Imaginary numbers, often represented by “i,” are numbers that, when squared, result in a negative number. At WHAT.EDU.VN, we simplify complex mathematical concepts like imaginary numbers, making them accessible and easy to understand. Delve into the realm of imaginary units, complex plane, and iota value.
1. What Are Imaginary Numbers?
Imaginary numbers are defined as multiples of the imaginary unit “i,” where i is the square root of -1 (i = √-1). This means that i² = -1. They are essential for working with the square roots of negative numbers, which do not exist within the set of real numbers.
To understand this better, let’s consider squaring real numbers:
- (-3)² = -3 × -3 = 9
- 4² = 4 × 4 = 16
- (2.5)² = 2.5 × 2.5 = 6.25
None of these results in a negative number. Squaring a real number always yields a positive result. So, where do negative squares come from? That’s where imaginary numbers come in.
Examples of imaginary numbers:
- √(-9) = √(-1) ⋅ √9 = i ⋅ 3 = 3i
- √(-5) = √(-1) ⋅ √5 = i√5
In these examples, 3i and i√5 are imaginary numbers. Each is the product of a non-zero real number and i. This leads to the general rule:
- √(-x) = i√x
Imaginary numbers form a part of complex numbers. A complex number is the sum of a real number and an imaginary number, typically expressed in the form a + bi, where ‘a’ and ‘b’ are real numbers, and ‘bi’ is the imaginary part.
2. The History of Imaginary Numbers
Imaginary numbers weren’t always readily accepted. Their journey from conception to acceptance involved the contributions of several mathematicians over centuries:
- 1st Century: Hero of Alexandria is often credited with the earliest, albeit indirect, reference to imaginary numbers while attempting to calculate the volume of a frustum (truncated pyramid). His calculations led to taking the square root of a negative number, which he simply dismissed as impossible.
- 16th Century: Gerolamo Cardano, an Italian mathematician, made significant strides by acknowledging imaginary numbers in his work Ars Magna (1545). While solving cubic equations, he encountered situations where he needed to manipulate square roots of negative numbers. Although he found them perplexing, he laid the groundwork for their algebraic manipulation.
- 17th Century: René Descartes, a French philosopher and mathematician, coined the term “imaginary” in 1637. However, he used it in a derogatory sense, implying that these numbers were unreal and existed only in the imagination.
- 18th Century: Abraham de Moivre and Roger Cotes played a role in developing complex number theory. However, it was Leonhard Euler who popularized the notation “i” for the square root of -1 in 1777. Euler’s work significantly legitimized imaginary numbers and integrated them into mainstream mathematics.
- 19th Century: Augustin-Louis Cauchy, Carl Friedrich Gauss, and Caspar Wessel helped establish the geometric interpretation of complex numbers. Gauss, in particular, introduced the term “complex number” and provided a formal definition, while Wessel was among the first to represent complex numbers as points in a plane. These developments solidified the place of imaginary numbers in mathematics by providing a visual and concrete representation.
The acceptance of imaginary numbers was gradual and met with skepticism, but their eventual integration into mathematics proved invaluable.
3. Geometrical Interpretation of Imaginary Numbers
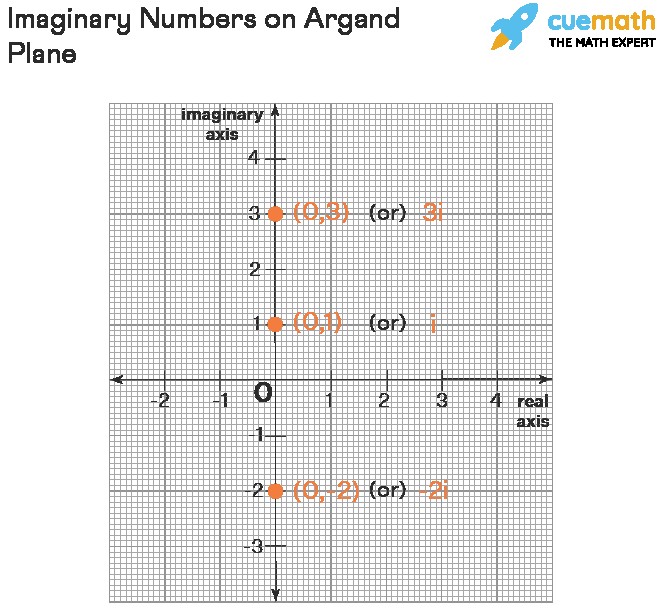
Complex numbers, including imaginary numbers, can be represented on the Argand plane (also known as the complex plane). In this plane, the horizontal axis represents the real part of the complex number, and the vertical axis represents the imaginary part.
A complex number a + bi is represented by the point (a, b) on the Argand plane. For example, the complex number 2 – 4i corresponds to the point (2, -4).
An imaginary number bi (which can be written as 0 + bi) is represented by the point (0, b). This means that imaginary numbers always lie on the vertical axis (imaginary axis) of the Argand plane.
4. What is the Significance of “i” in Math?
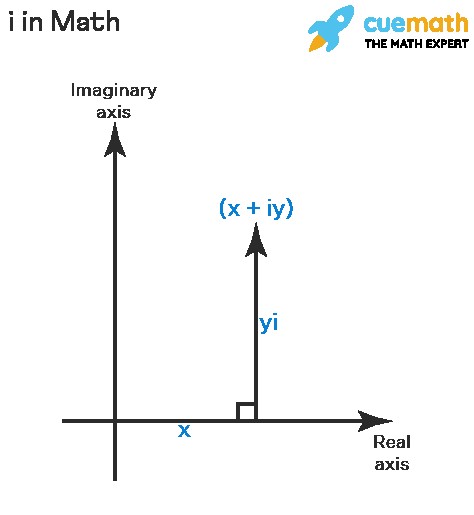
In the complex number x + iy, corresponding to the point P(x, y), “i” cannot be a real number. If i were real, then x + iy would also be real and would lie on the real axis. Thus, i must be a non-real number, not belonging to the Real set.
We interpret i in math as “one unit in the direction perpendicular to the real axis.” In the Argand plane, the point (0, 1) represents “i.”
Therefore, in the complex number x + iy, the term iy represents y times i, which means y units in the i direction. The entire expression x + iy represents a point that can be reached by moving x units in the Real direction and y units in the i direction from the origin.
4.1 The Value of i
Arithmetically, i² = -1. The value of i is the square root of -1. This is a foundational concept in complex numbers.
Keep in mind that:
- i is a non-real number, lying outside the Real set.
- i represents one unit perpendicular to the Real direction.
- yi represents y units perpendicular to the Real direction.
- x + iy represents the point (x, y) on the complex plane.
- i is the square root of -1, or i² = -1.
When we say that i is a non-real number, it doesn’t mean that i doesn’t exist or is just a figment of our imagination. It means that i is non-real in the sense that it does not lie in the Real set. However, it is a perfectly valid mathematical entity, also known as “iota.”
5. How to Perform Calculations with Imaginary Numbers
Calculations with imaginary numbers follow similar rules to those used with real numbers.
5.1 Adding and Subtracting Imaginary Numbers
Adding or subtracting imaginary numbers is similar to combining like terms in algebra:
- 5i + 2i = 7i
- 8i – 3i = 5i
5.2 Multiplying Imaginary Numbers
When multiplying imaginary numbers, use the same rules as multiplying algebraic terms. Remember that i² = -1:
- 4i × 2i = 8i² = 8(-1) = -8
- -2i² × 6i³ = -12i⁵ = -12(i²)²i = -12(-1)²i = -12i
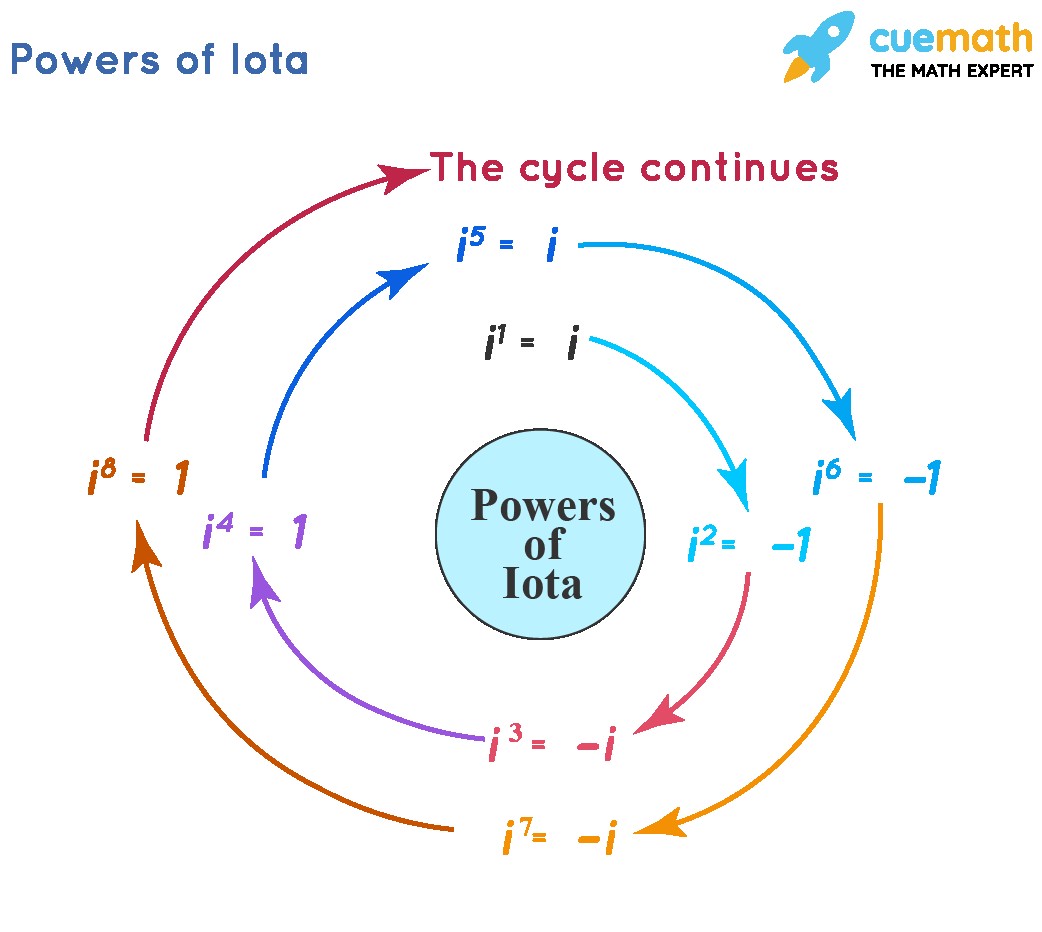
Simplifying powers of iota can be made easier with these rules:
- i^(4k) = 1
- i^(4k+1) = i
- i^(4k+2) = -1
- i^(4k+3) = -i
where k is a whole number. These rules indicate that i raised to any power is equal to i raised to the remainder obtained by dividing the original power by 4. For example:
- i⁴ = i⁰ = 1
- i¹⁸ = i² = -1
Any power of i simplifies to one of 1, i, -i, or -1.
5.3 Dividing Imaginary Numbers
When dividing imaginary numbers, use the exponent rule a^m / a^n = a^(m-n). It’s standard practice to avoid having “i” in the denominator. If it appears, use the rule 1/i = -i:
- 6i / 3i = 2
- 5i³ / 2i⁵ = 5 / (2i²) = 5 / (2(-1)) = -5/2
6. Real-World Applications of Imaginary Numbers
While imaginary numbers might seem abstract, they have practical applications in various fields:
- Electrical Engineering: Used to analyze alternating current (AC) circuits, where voltage and current oscillate. Impedance, which is the AC equivalent of resistance, is expressed using complex numbers.
- Quantum Mechanics: Essential for describing the behavior of particles at the subatomic level. The wave function, which describes the state of a particle, is a complex-valued function.
- Signal Processing: Used in the analysis and design of filters and other signal processing algorithms.
- Fluid Dynamics: Helps in solving problems related to fluid flow, particularly in aerodynamics and hydrodynamics.
- Control Systems: Used to analyze and design control systems, which are used to regulate the behavior of dynamic systems.
- Fractals: The Mandelbrot set, a famous fractal, is defined using complex numbers.
7. Tips and Tricks for Working with Imaginary Numbers
- When a minus sign comes out of the square root, it becomes i because i = √(-1).
- √n can be simplified using imaginary numbers when x is negative and n is an even number.
- When “i” is in the denominator, use the rule 1/i = -i.
- i^n = i^r, where ‘r’ is the remainder obtained by dividing n by 4. Apply the rules: i² = -1, i³ = -i, i⁴ = 1.
8. Examples of Imaginary Number Problems
Example 1: Simplify (4i)²
Solution:
(4i)² = (4i)(4i) = 16i² = 16(-1) = -16
Answer: (4i)² = -16
Example 2: Express the roots of the quadratic equation x² + 2x + 5 = 0 in terms of imaginary numbers.
Solution:
Using the quadratic formula:
x = (-b ± √(b² – 4ac)) / (2a)
Comparing with ax² + bx + c = 0, we get a = 1, b = 2, and c = 5.
x = (-2 ± √(2² – 4 1 5)) / (2 * 1)
x = (-2 ± √(4 – 20)) / 2
x = (-2 ± √(-16)) / 2
x = (-2 ± 4i) / 2
x = -1 ± 2i
Answer: The roots are -1 + 2i and -1 – 2i.
Example 3: Find the values of (a) i¹²⁵ and (b) i⁻²⁰³.
Solution:
(a) i¹²⁵ = i¹ = i (since 125 ÷ 4 leaves a remainder of 1)
(b) i⁻²⁰³ = 1 / i²⁰³ = 1 / i³ = 1 / -i = i (since 203 ÷ 4 leaves a remainder of 3, and 1/-i = i)
Answers: (a) i¹²⁵ = i, (b) i⁻²⁰³ = i
9. FAQ on Imaginary Numbers
| Question | Answer |
|---|---|
| What is the definition of imaginary numbers? | An imaginary number is a number that is the product of a non-zero real number and the imaginary unit “i,” where i = √(-1) or i² = -1. These numbers are used to find the square root of negative numbers. Examples include -5i, 7i, and i. |
| What is the value of i in math? | “i” is known as an imaginary unit. Its value is √-1. It is used to calculate the square roots of negative numbers and is a part of complex numbers. |
| How do you simplify imaginary numbers? | To add/subtract imaginary numbers, simply add/subtract their coefficients (e.g., -3i + 9i – 5i = i). To multiply/divide, use algebraic rules, remembering that i² = -1 and 1/i = -i. |
| What is the difference between imaginary and complex numbers? | An imaginary number is in the form bi, while a complex number is in the form a + bi, where a and b are real numbers. All imaginary numbers are complex numbers (where a can be 0), but not all complex numbers are imaginary numbers. |
| What is the difference between imaginary and real numbers? | A real number can be a natural number, whole number, integer, rational number, or irrational number. An imaginary number is the product of a real number and “i,” where i = √(-1). Imaginary numbers are used to evaluate the square root of negative numbers (e.g., √(-16) = √(-1) ⋅ √16 = i(4) = 4i). |
| What are the basic rules for imaginary numbers? | The basic rules include: i = √(-1), i² = -1, i³ = -i, i⁴ = 1, i^n = i^r (where r is the remainder when n is divided by 4), and 1/i = -i (useful for negative powers of i). |
| How can a real number be written in terms of i? | Any real number x can be written as x + i0. Real numbers can be considered complex numbers where the non-real part is 0. The Real set is a subset of the Complex set. |
| Is 0 an imaginary number? | Although 0 can be written as 0i, it is not considered an imaginary number because it is not associated with the square root of any negative number. Imaginary numbers are defined as bi where ‘b’ is a non-zero real number. |
| What are the applications of Imaginary Numbers? | Imaginary numbers are used in electrical engineering, quantum mechanics, signal processing, fluid dynamics, control systems, and fractals. For example, they help in analyzing alternating current (AC) circuits, describing the behavior of particles at the subatomic level, and designing filters for signal processing algorithms. |
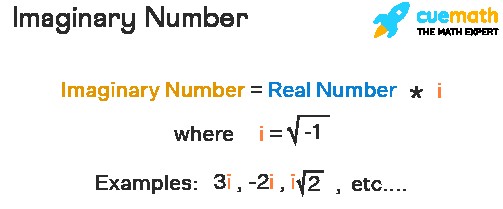

10. Conclusion
Imaginary numbers, though initially perplexing, are a fundamental part of mathematics with significant real-world applications. Understanding what “i” is in math and how to work with imaginary numbers opens up new possibilities in various scientific and engineering fields.
Do you have more questions about imaginary numbers or other math topics? Visit WHAT.EDU.VN today and get your questions answered for free. Our experts are ready to help you understand even the most complex concepts. Contact us at 888 Question City Plaza, Seattle, WA 98101, United States, or via WhatsApp at +1 (206) 555-7890. Don’t hesitate – unlock your mathematical potential with what.edu.vn!