Isosceles Triangle: Understanding Its Definition and Properties. Are you curious about isosceles triangles and their unique characteristics? At WHAT.EDU.VN, we provide a clear explanation of What Is Isosceles Triangle, and delve into its properties and significance. Discover its definition, explore its angle relationships, and see how it differs from other triangles. Delve into triangle geometry, explore its attributes, and unlock its importance.
1. Defining the Isosceles Triangle: A Comprehensive Overview
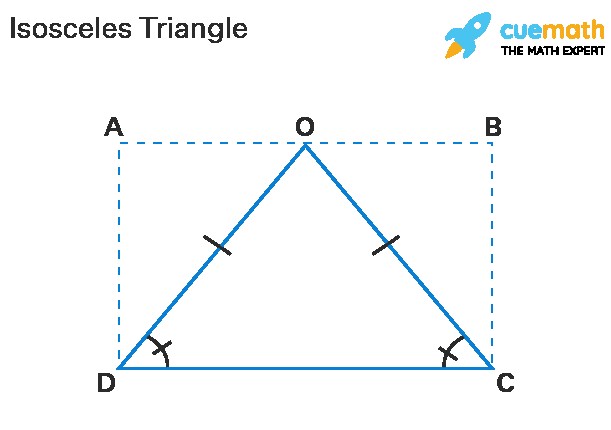
An isosceles triangle is a fundamental geometric shape characterized by having two sides of equal length. This seemingly simple condition leads to a wealth of interesting properties and relationships, making the isosceles triangle a fascinating subject of study in geometry. Delving into the definition of an isosceles triangle is essential for grasping its characteristics and applications.
1.1. Core Characteristics: Equal Sides and Base Angles
The defining feature of an isosceles triangle is the presence of two sides with the same length. These sides are commonly referred to as the legs of the triangle, while the third side, which may or may not be equal in length to the legs, is called the base.
1.1.1. Base Angles: The Foundation of Symmetry
A direct consequence of having two equal sides is that the angles opposite those sides, known as the base angles, are also equal in measure. This property is a cornerstone of isosceles triangle geometry and is formally stated by the Isosceles Triangle Theorem.
1.2. The Isosceles Triangle Theorem: A Formal Statement
The Isosceles Triangle Theorem states that if two sides of a triangle are congruent (equal in length), then the angles opposite those sides are congruent (equal in measure). Conversely, the theorem also holds in reverse: if two angles of a triangle are congruent, then the sides opposite those angles are congruent.
1.2.1. Converse of the Theorem: A Two-Way Street
The converse of the Isosceles Triangle Theorem is equally important. It states that if two angles of a triangle are equal, then the sides opposite those angles are also equal. This converse allows us to identify isosceles triangles based on their angle measurements.
1.3. Exploring Variations: Isosceles Right Triangles
While the basic definition focuses on equal sides, isosceles triangles can also be classified based on their angles. One special type is the isosceles right triangle, which combines the properties of both isosceles and right triangles.
1.3.1. Isosceles Right Triangle: A Unique Combination
An isosceles right triangle is a triangle that has two equal sides and one right angle (90 degrees). The two equal sides form the legs of the right triangle, and the angles opposite those legs are both 45 degrees. This specific combination of properties makes the isosceles right triangle a valuable tool in various geometric and trigonometric applications.
2. Unveiling the Properties of Isosceles Triangles
Beyond the basic definition, isosceles triangles possess a range of unique properties that distinguish them from other types of triangles. These properties relate to their sides, angles, symmetry, and area, offering insights into their geometric behavior.
2.1. Sides and Angles: Interconnected Relationships
The equal sides and base angles of an isosceles triangle are intrinsically linked. The Isosceles Triangle Theorem highlights this connection, stating that equal sides imply equal opposite angles and vice versa.
2.1.1. Equal Sides Imply Equal Angles: A Fundamental Rule
As previously discussed, the Isosceles Triangle Theorem is a cornerstone of isosceles triangle geometry. Knowing that two sides are equal immediately tells us that the angles opposite those sides are also equal.
2.1.2. Equal Angles Imply Equal Sides: The Converse in Action
Conversely, if we know that two angles in a triangle are equal, we can confidently conclude that the sides opposite those angles are also equal, making the triangle an isosceles triangle.
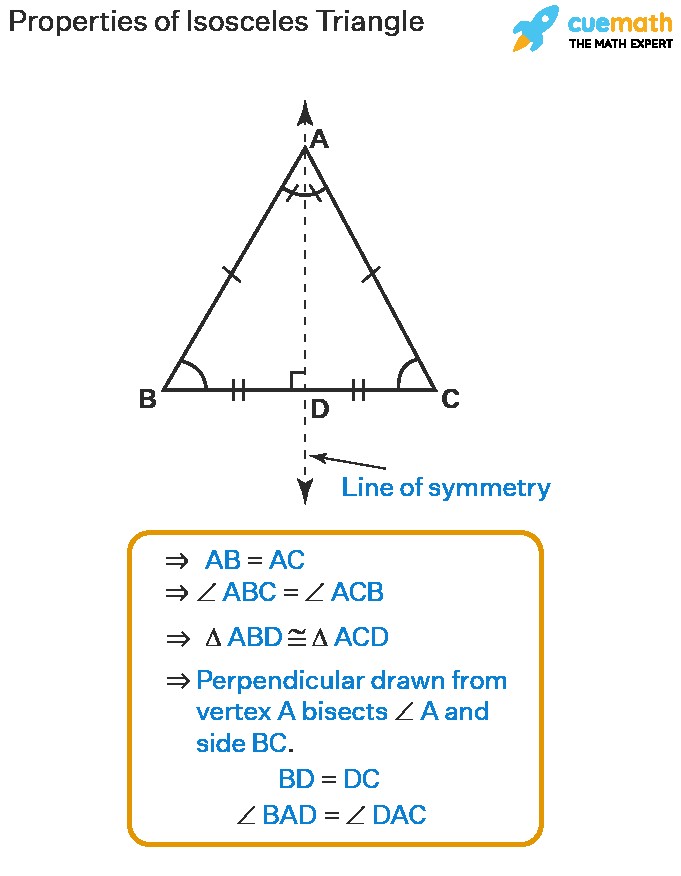
2.2. Symmetry: A Defining Characteristic
Isosceles triangles exhibit a distinct symmetry around a line that bisects the vertex angle (the angle formed by the two equal sides) and the base. This line of symmetry divides the isosceles triangle into two congruent right triangles.
2.2.1. Line of Symmetry: Dividing the Triangle in Half
The line of symmetry in an isosceles triangle has several important properties:
- It bisects the vertex angle, dividing it into two equal angles.
- It bisects the base, dividing it into two equal segments.
- It is perpendicular to the base, forming a right angle.
- It acts as both a median and an altitude of the triangle.
2.3. Area Calculation: Utilizing Base and Height
The area of an isosceles triangle can be calculated using the standard formula for the area of a triangle:
Area = 1/2 base height
2.3.1. Determining the Height: Using the Pythagorean Theorem
If the height is not directly given, it can be calculated using the Pythagorean Theorem, since the line of symmetry divides the isosceles triangle into two congruent right triangles.
2.4. Perimeter Calculation: Summing the Sides
The perimeter of an isosceles triangle is simply the sum of the lengths of its three sides. Given that two sides are equal, the perimeter can be expressed as:
Perimeter = 2 * (length of equal side) + (length of base)
3. Understanding Isosceles Triangle Angles
The angles within an isosceles triangle are crucial to understanding its geometry. The relationships between the base angles and the vertex angle, as well as the possible angle combinations, define the overall shape and properties of the triangle.
3.1. Base Angles: Always Equal
The defining characteristic of isosceles triangle angles is that the two base angles are always equal in measure. This equality is a direct consequence of the Isosceles Triangle Theorem.
3.1.1. Measuring Base Angles: Key to Triangle Properties
Knowing the measure of one base angle immediately tells us the measure of the other. This information, along with the fact that the sum of all angles in a triangle is 180 degrees, allows us to determine the measure of the vertex angle.
3.2. Vertex Angle: Dependent on Base Angles
The vertex angle, formed by the two equal sides, is directly dependent on the measures of the base angles. Since the sum of all angles in a triangle is 180 degrees, the vertex angle can be calculated as follows:
Vertex Angle = 180 degrees – 2 * (measure of base angle)
3.2.1. Calculating Vertex Angle: The Angle Sum Property
This formula highlights the relationship between the base angles and the vertex angle. If the base angles are small, the vertex angle will be large, and vice versa.
3.3. Possible Angle Combinations: Acute, Right, and Obtuse
Isosceles triangles can be classified as acute, right, or obtuse, depending on the measure of their largest angle:
- Acute Isosceles Triangle: All three angles are less than 90 degrees.
- Right Isosceles Triangle: One angle is exactly 90 degrees (and the other two are 45 degrees).
- Obtuse Isosceles Triangle: One angle is greater than 90 degrees.
3.3.1. Classifying Isosceles Triangles: Angle Measurement is Key
The angle classification depends on the measure of the vertex angle. If the vertex angle is less than 90 degrees, the triangle is acute. If it is exactly 90 degrees, the triangle is right. If it is greater than 90 degrees, the triangle is obtuse.
4. Differentiating Isosceles, Scalene, and Equilateral Triangles
Isosceles triangles are part of a broader family of triangles, which can be classified based on their side lengths and angle measures. Understanding the differences between isosceles, scalene, and equilateral triangles is crucial for a complete understanding of triangle geometry.
4.1. Scalene Triangles: No Equal Sides
Scalene triangles are characterized by having no sides of equal length. As a result, all three angles in a scalene triangle are also different in measure.
4.1.1. Scalene Triangle Properties: All Sides and Angles Differ
The lack of equal sides and angles distinguishes scalene triangles from both isosceles and equilateral triangles.
4.2. Equilateral Triangles: All Sides Equal
Equilateral triangles are the most symmetrical type of triangle. All three sides are equal in length, and all three angles are equal in measure (60 degrees each).
4.2.1. Equilateral Triangle Properties: Perfect Symmetry
The perfect symmetry of equilateral triangles leads to numerous special properties, making them a fundamental shape in geometry and other fields.
4.3. Comparison Table: Key Differences
| Feature | Scalene Triangle | Isosceles Triangle | Equilateral Triangle |
|---|---|---|---|
| Equal Sides | None | Two | Three |
| Equal Angles | None | Two | Three (60 degrees each) |
| Symmetry | None | One line of symmetry | Three lines of symmetry |
| General Definition | No equal sides | At least two equal sides | All sides equal |
4.3.1. Understanding Triangle Classification: Side and Angle Relationships
This comparison table highlights the key differences between the three types of triangles, emphasizing the importance of side and angle relationships in classifying triangles.
5. Exploring Isosceles Triangle Examples
To solidify your understanding of isosceles triangles, let’s examine a few examples that showcase their properties and applications.
5.1. Example 1: Finding a Missing Angle
In an isosceles triangle, one of the base angles measures 55 degrees. Find the measure of the vertex angle.
Solution:
Since the triangle is isosceles, the other base angle also measures 55 degrees. The sum of all angles in a triangle is 180 degrees. Therefore:
Vertex Angle = 180 degrees – 55 degrees – 55 degrees = 70 degrees
5.2. Example 2: Calculating the Area
An isosceles triangle has a base of 12 cm and equal sides of 10 cm each. Find the area of the triangle.
Solution:
First, we need to find the height of the triangle. The height bisects the base, creating two right triangles with a base of 6 cm and a hypotenuse of 10 cm. Using the Pythagorean Theorem:
height = √(10^2 – 6^2) = √(100 – 36) = √64 = 8 cm
Now, we can calculate the area:
Area = 1/2 base height = 1/2 12 cm 8 cm = 48 square cm
5.3. Example 3: Identifying Isosceles Triangles
A triangle has angles measuring 40 degrees, 70 degrees, and 70 degrees. Is this triangle an isosceles triangle?
Solution:
Yes, this triangle is an isosceles triangle. It has two angles that are equal (70 degrees each), which means the sides opposite those angles are also equal.
6. Frequently Asked Questions (FAQs) About Isosceles Triangles
To address common queries and provide further clarification, here’s a collection of frequently asked questions about isosceles triangles.
6.1. What Exactly Defines an Isosceles Triangle?
An isosceles triangle is defined as a triangle with at least two sides of equal length. This defining characteristic leads to several unique properties, including equal base angles.
6.2. What is the Significance of the Isosceles Triangle Theorem?
The Isosceles Triangle Theorem states that if two sides of a triangle are congruent, then the angles opposite those sides are congruent. This theorem is fundamental to understanding the relationships between sides and angles in isosceles triangles.
6.3. How Can I Determine if a Triangle is Isosceles?
A triangle can be identified as isosceles if it meets one of the following criteria:
- It has two sides of equal length.
- It has two angles of equal measure.
6.4. Do Isosceles Triangles Always Have Equal Angles?
Isosceles triangles always have two equal angles, known as the base angles. The third angle, the vertex angle, may or may not be equal to the base angles.
6.5. What Angle Combinations are Possible in Isosceles Triangles?
Isosceles triangles can have various angle combinations, as long as two angles are equal and the sum of all three angles is 180 degrees. This includes acute, right, and obtuse isosceles triangles.
6.6. What is the Defining Feature of a Right-Angled Isosceles Triangle?
A right-angled isosceles triangle has one angle that measures 90 degrees (a right angle) and two equal sides. The two equal sides form the legs of the right angle, and the other two angles each measure 45 degrees.
6.7. Is it Possible for an Isosceles Triangle to be a Right Triangle?
Yes, it is possible for an isosceles triangle to be a right triangle. In this case, the two equal sides form the legs of the right angle, and the other two angles each measure 45 degrees.
6.8. What Formula is Used to Calculate the Area of an Isosceles Triangle?
The area of an isosceles triangle can be calculated using the standard formula for the area of a triangle: Area = 1/2 base height. The height can be determined using the Pythagorean Theorem if it is not directly given.
6.9. Can You List the Key Properties of Isosceles Triangles?
Key properties of isosceles triangles include:
- Two sides of equal length.
- Two angles of equal measure (base angles).
- A line of symmetry that bisects the vertex angle and the base.
- The line of symmetry is perpendicular to the base.
6.10. How is the Perimeter of an Isosceles Triangle Calculated?
The perimeter of an isosceles triangle is calculated by summing the lengths of all three sides. Given that two sides are equal, the perimeter can be expressed as: Perimeter = 2 * (length of equal side) + (length of base).
6.11. What is Considered the Vertex Angle in an Isosceles Triangle?
The vertex angle in an isosceles triangle is the angle formed by the two equal sides. It is opposite the base of the triangle.
6.12. How is the Base Defined in an Isosceles Triangle?
The base of an isosceles triangle is the side that is not necessarily equal to the other two sides. It is opposite the vertex angle.
7. Test Your Knowledge: Isosceles Triangle Questions
Put your understanding of isosceles triangles to the test with these practice questions.
- Two sides of an isosceles triangle are 8 cm and 15 cm. What is the length of the third side?
- The perimeter of an isosceles triangle is 60 cm. If one of the equal sides measures 18 cm, find the measure of the non-equal side.
- An isosceles triangle has an angle measuring 120 degrees. What are the measures of the remaining two angles?
- An isosceles triangle has a base of 10 m and a height of 7 m. What is the area of the triangle?
- If the base of an isosceles triangle is equal to its height, what is the 25% area of the triangle?
Scroll down for answers
Answers:
- 8 cm or 15 cm (two possibilities)
- 24 cm
- 30 degrees each
- 35 square meters
- 1/8 the area of the triangle
Do you have more questions about isosceles triangles or any other topic? Visit WHAT.EDU.VN today and ask your questions for free! Our community of experts is ready to provide you with clear and helpful answers.
Contact Us:
Address: 888 Question City Plaza, Seattle, WA 98101, United States
Whatsapp: +1 (206) 555-7890
Website: what.edu.vn
Don’t hesitate to reach out and get the answers you need!