The quotient is the result you get when you divide one number by another, a foundational concept in mathematics. At WHAT.EDU.VN, we help you understand this mathematical operation and its applications. Discover how to calculate and interpret quotients with ease and enhance your understanding of division problems, division operation, and related math concepts.
1. What Is the Quotient? The Result of Division
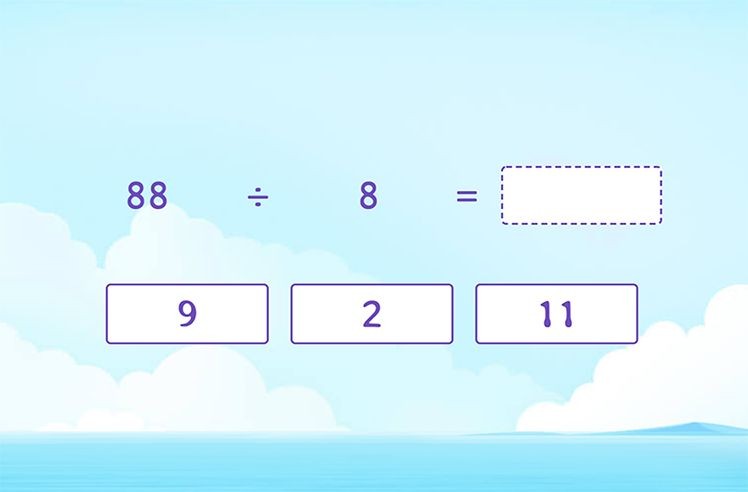
The quotient is the numerical value derived from dividing one number (the dividend) by another (the divisor). Essentially, it tells you how many times the divisor fits into the dividend. The quotient is a fundamental concept in arithmetic.
For instance, in the equation 10 ÷ 2 = 5, the quotient is 5. Here, 10 represents the dividend, and 2 is the divisor.
Consider these key points:
- The dividend is the number being divided.
- The divisor is the number by which the dividend is divided.
- The quotient is the result of the division.
To delve deeper into this understanding, let’s consider various forms of the quotient and how to calculate it through different methods.
2. Exploring Different Forms of Quotients
The quotient is not always a whole number; it can take various forms, including integers and decimals.
2.1. Integer Quotients: Complete Division
When one number is perfectly divisible by another, the resulting quotient is a whole number, also known as an integer. For example:
- 12 ÷ 3 = 4
Here, the quotient 4 is an integer because 12 is completely divisible by 3, leaving no remainder. Integer quotients are common in basic division problems and represent scenarios where division is clean and straightforward.
2.2. Decimal Quotients: Incomplete Division
In cases where a number is not completely divisible by another, the quotient is expressed as a decimal number. For example:
- 13 ÷ 2 = 6.5
In this scenario, the quotient 6.5 is a decimal because 13 cannot be divided evenly by 2. Decimal quotients indicate that the division results in a fractional part, providing a more precise answer than whole numbers alone.
2.3. Quotient with Remainder: An Alternative Representation
When a division problem results in a remainder, there is an alternative way to express the answer:
- 23 ÷ 4 = 5 R 3
Here, the quotient is 5, and the remainder is 3. This notation means that 4 goes into 23 five times with 3 left over. This method is particularly useful in scenarios where the fractional part of the division is less important than understanding the whole number result and the leftover amount.
Understanding these different forms of quotients allows for a more versatile and accurate approach to solving division problems in various contexts.
3. Methods to Calculate the Quotient
Several methods can be employed to calculate the quotient, each offering a unique approach suitable for different situations.
3.1. Repeated Subtraction
Repeated subtraction is a basic method to understand division, especially for those new to the concept. It involves repeatedly subtracting the divisor from the dividend until you reach zero or a number less than the divisor. The number of times you subtract is the quotient.
Let’s illustrate this with an example:
Find the quotient of 15 ÷ 3 using repeated subtraction.
- 15 – 3 = 12
- 12 – 3 = 9
- 9 – 3 = 6
- 6 – 3 = 3
- 3 – 3 = 0
We subtracted 3 five times to reach 0, therefore, the quotient is 5.
Repeated subtraction is an intuitive way to grasp the concept of division, making it easier to understand more complex methods.
3.2. Long Division Method
Long division is a standard algorithm used to divide large numbers. It breaks down the division process into manageable steps: Divide, Multiply, Subtract, Bring Down, and Repeat (or Remainder).
Here’s how to perform long division with an example:
Divide 185 by 5.
- Divide: Divide the first digit(s) of the dividend (18) by the divisor (5). 18 ÷ 5 = 3 (the first digit of the quotient).
- Multiply: Multiply the quotient digit (3) by the divisor (5). 3 × 5 = 15.
- Subtract: Subtract the result (15) from the divided portion of the dividend (18). 18 – 15 = 3.
- Bring Down: Bring down the next digit of the dividend (5) to form the new dividend (35).
- Repeat: Repeat the process with the new dividend (35).
- Divide: 35 ÷ 5 = 7 (the next digit of the quotient).
- Multiply: 7 × 5 = 35.
- Subtract: 35 – 35 = 0.
Since there are no more digits to bring down and the remainder is 0, the long division is complete. The quotient is 37.
Long division provides a structured approach to solving division problems, especially useful for multi-digit numbers.
3.3. Using a Calculator
For quick and accurate calculations, especially with decimal quotients or large numbers, a calculator is an invaluable tool. Simply enter the dividend, press the division key (÷), enter the divisor, and press the equals key (=) to display the quotient.
For example:
To find the quotient of 256 ÷ 7, enter 256 ÷ 7 = , which results in approximately 36.571.
Calculators save time and reduce errors, making them essential for practical applications and complex calculations.
4. Real-World Applications of the Quotient
The concept of the quotient extends beyond simple arithmetic and is crucial in numerous real-world applications.
4.1. Everyday Scenarios
In everyday life, quotients help us solve problems related to sharing, distribution, and measurement. Here are a few examples:
- Sharing: If you have 24 candies to share equally among 6 friends, the quotient (24 ÷ 6 = 4) tells you each friend gets 4 candies.
- Cooking: A recipe requires 3 cups of flour for one cake. If you have 15 cups of flour, the quotient (15 ÷ 3 = 5) tells you how many cakes you can bake.
- Travel: If you drive 300 miles in 6 hours, the quotient (300 ÷ 6 = 50) gives you your average speed in miles per hour.
- Budgeting: If you earn $2000 a month and need to allocate it among 5 categories, the quotient ($2000 ÷ 5 = $400) shows how much to allocate to each category.
Quotients provide a clear and concise way to handle everyday situations involving division, making calculations straightforward and practical.
4.2. Business and Finance
In the business and finance world, quotients are essential for calculating ratios, margins, and other key performance indicators. Consider these applications:
- Profit Margin: If a company has a revenue of $500,000 and a net profit of $50,000, the profit margin (50,000 ÷ 500,000 = 0.1 or 10%) is a quotient that indicates profitability.
- Inventory Turnover: A store with $200,000 in sales and an average inventory value of $40,000 has an inventory turnover ratio (200,000 ÷ 40,000 = 5). This quotient shows how many times the inventory is sold and replaced during a period. According to a study by the Retail Owners Institute in 2024, a higher turnover rate often correlates with better sales efficiency.
- Return on Investment (ROI): An investment that generates $10,000 in profit from an initial investment of $100,000 has an ROI (10,000 ÷ 100,000 = 0.1 or 10%). This quotient is crucial for evaluating the efficiency of investments.
Quotients offer critical insights into financial performance, helping businesses make informed decisions and improve their bottom line.
4.3. Scientific and Engineering Fields
Quotients play a vital role in scientific and engineering calculations, helping to determine rates, proportions, and other essential metrics. Here are a few examples:
- Density Calculation: Density is calculated by dividing mass by volume (Density = Mass ÷ Volume). For instance, if an object has a mass of 500 grams and a volume of 250 cubic centimeters, its density (500 ÷ 250 = 2 grams per cubic centimeter) is a quotient.
- Speed and Velocity: Speed is calculated by dividing the distance traveled by the time taken (Speed = Distance ÷ Time). If a car travels 150 miles in 3 hours, its average speed (150 ÷ 3 = 50 miles per hour) is a quotient.
- Scale Factors in Engineering: When creating scaled models, engineers use quotients to maintain proportions. For example, if a building is 50 meters tall and its model is 0.5 meters tall, the scale factor (0.5 ÷ 50 = 0.01) is a quotient that helps ensure accuracy.
- Fluid Dynamics: In fluid dynamics, the flow rate is often calculated as the volume of fluid passing a point per unit of time. If 10 liters of water flow through a pipe in 2 minutes, the flow rate (10 ÷ 2 = 5 liters per minute) is a quotient.
These examples highlight the indispensable role of quotients in providing quantitative data and enabling precise analysis in various scientific and engineering contexts.
5. How the Quotient Differs From Other Division Terms
Understanding the different terms related to division can help clarify the concept of the quotient.
5.1. Quotient vs. Dividend
- Dividend: The number being divided. It is the total quantity that you want to split into equal parts.
- Quotient: The result obtained after dividing the dividend by the divisor. It represents how many times the divisor fits into the dividend.
For example, in the equation 20 ÷ 4 = 5:
- 20 (the number being divided) is the dividend.
- 5 (the result of the division) is the quotient.
The dividend is the starting point, while the quotient is the result of the division process.
5.2. Quotient vs. Divisor
- Divisor: The number by which the dividend is divided. It determines the number of equal parts the dividend will be split into.
- Quotient: As mentioned, the result obtained after dividing the dividend by the divisor.
In the same equation, 20 ÷ 4 = 5:
- 4 (the number dividing the dividend) is the divisor.
- 5 (the result of the division) is the quotient.
The divisor determines the size of the groups, while the quotient indicates how many of those groups there are.
5.3. Quotient vs. Remainder
- Remainder: The amount left over when the dividend cannot be divided evenly by the divisor. It is the portion that remains after performing the division.
- Quotient: Again, the result obtained after dividing the dividend by the divisor.
Consider the equation 23 ÷ 4 = 5 with a remainder of 3:
- 5 is the quotient (how many times 4 fully goes into 23).
- 3 is the remainder (the amount left over because 23 is not perfectly divisible by 4).
The remainder is what’s left after dividing as much as possible, while the quotient is the result of the division before considering any leftover amount.
5.4. Quotient vs. Product
- Product: The result of multiplying two numbers. It is the total when you combine equal groups.
- Quotient: The result of dividing two numbers, indicating how many times one number fits into another.
For example:
- Multiplication: 3 × 4 = 12 (12 is the product).
- Division: 12 ÷ 4 = 3 (3 is the quotient).
The product is the result of combining quantities, while the quotient is the result of splitting a quantity into equal parts. These terms represent opposite operations but are fundamental in mathematical calculations.
6. Verify Quotient in Division
Verifying the quotient is essential to ensure accuracy. The basic formula to verify a division is:
Dividend = (Divisor × Quotient) + Remainder
Let’s break this down with examples:
6.1. Example 1: No Remainder
Consider the division 36 ÷ 6 = 6.
- Dividend = 36
- Divisor = 6
- Quotient = 6
- Remainder = 0
Using the formula:
36 = (6 × 6) + 0
36 = 36 + 0
36 = 36
This confirms that the quotient is correct since the equation holds true.
6.2. Example 2: With Remainder
Consider the division 47 ÷ 9 = 5 with a remainder of 2.
- Dividend = 47
- Divisor = 9
- Quotient = 5
- Remainder = 2
Using the formula:
47 = (9 × 5) + 2
47 = 45 + 2
47 = 47
Again, the equation holds true, verifying that the quotient and remainder are correct.
6.3. Example 3: Checking Decimal Quotients
Consider the division 25 ÷ 4 = 6.25.
- Dividend = 25
- Divisor = 4
- Quotient = 6.25
- Remainder = 0 (since it’s a decimal quotient)
Using the formula:
25 = (4 × 6.25) + 0
25 = 25 + 0
25 = 25
The equation is true, validating the decimal quotient.
Regular verification ensures accuracy and builds confidence in your division calculations.
7. Frequently Asked Questions About Quotient
To further clarify the concept of the quotient, here are some frequently asked questions:
7.1. What is the quotient in math?
In mathematics, the quotient is the result you get when you divide one number (the dividend) by another number (the divisor). It tells you how many times the divisor fits into the dividend. For example, in 15 ÷ 3 = 5, the quotient is 5.
7.2. How do you find the quotient?
You can find the quotient using several methods:
- Repeated Subtraction: Subtract the divisor from the dividend until you reach zero or a number less than the divisor. The number of subtractions is the quotient.
- Long Division: Use the long division algorithm to divide the dividend by the divisor step by step.
- Calculator: Use a calculator to perform the division, especially for larger numbers or decimals.
7.3. What is the difference between the quotient and the product?
The quotient is the result of division, while the product is the result of multiplication. Division and multiplication are inverse operations. For example:
- Quotient: 12 ÷ 4 = 3
- Product: 3 × 4 = 12
7.4. What are the different parts of a division problem?
The different parts of a division problem are:
- Dividend: The number being divided.
- Divisor: The number by which the dividend is divided.
- Quotient: The result of the division.
- Remainder: The amount left over if the dividend is not evenly divisible by the divisor.
7.5. Can the quotient be a fraction or a decimal?
Yes, the quotient can be a fraction or a decimal if the dividend is not evenly divisible by the divisor. For example:
- 10 ÷ 3 = 3.333… (decimal)
- 5 ÷ 2 = 2 1/2 (fraction)
7.6. What happens if the divisor is zero?
Division by zero is undefined in mathematics. You cannot divide any number by zero because it leads to logical inconsistencies.
7.7. How does the quotient relate to remainders?
The quotient and remainder together provide a complete answer to a division problem. The quotient tells you how many times the divisor fits into the dividend completely, and the remainder tells you what is left over. The relationship can be expressed as:
Dividend = (Divisor × Quotient) + Remainder
7.8. Is the quotient always smaller than the dividend?
No, the quotient is not always smaller than the dividend. This is true when the divisor is greater than 1. However, if the divisor is less than 1, the quotient will be larger than the dividend. For example:
- 10 ÷ 2 = 5 (quotient is smaller)
- 10 ÷ 0.5 = 20 (quotient is larger)
7.9. How do I verify that my quotient is correct?
To verify your quotient, use the formula:
Dividend = (Divisor × Quotient) + Remainder
If the equation holds true, your quotient is correct.
7.10. Where can I get help with understanding quotients and division?
For additional help with understanding quotients and division, you can visit WHAT.EDU.VN, where you can ask questions and receive free answers to enhance your mathematical knowledge.
By understanding the quotient and related division terms, you can confidently tackle various mathematical problems in both academic and real-world contexts.
Do you have more questions about the quotient or other math topics? Visit what.edu.vn and ask your questions for free. Our community of experts is ready to provide clear, helpful answers to assist you with your learning needs. Contact us at 888 Question City Plaza, Seattle, WA 98101, United States, or reach out via Whatsapp at +1 (206) 555-7890. Start asking and learning today!