Are you struggling to understand what a quotient is in math? Look no further! At WHAT.EDU.VN, we break down complex mathematical concepts into easily digestible information. This comprehensive guide will help you understand the quotient definition, how to find it, and its relationship to other mathematical terms like divisor, dividend, and remainder. Unlock mathematical proficiency and conquer division with ease!
1. What is Quotient in Division?
The quotient is the result you get when you divide one number by another. In simpler terms, it’s the answer to a division problem. Division is a mathematical operation that involves splitting a whole into equal groups. For instance, if you have 15 cookies and want to divide them equally among 3 friends, each friend would get 5 cookies. Here, 5 is the quotient.
2. Quotient Definition
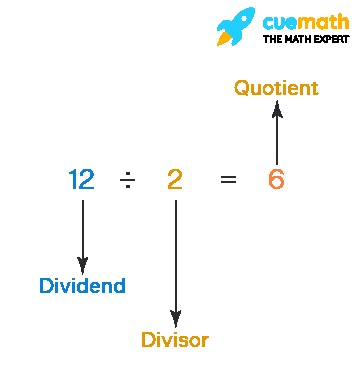
In mathematics, the quotient is defined as the number resulting from the division of one number (the dividend) by another (the divisor). It represents how many times the divisor is contained within the dividend. As shown in the image below, the dividend is the number being divided, the divisor is the number dividing it, and the quotient is the result. The quotient is usually smaller than the dividend, but can be larger or smaller than the divisor.
3. How to Find the Quotient
Finding the quotient involves performing the operation of division. Division is one of the four basic mathematical operations, along with addition, subtraction, and multiplication. The quotient is the end result of the division process. After a complete division, you obtain the quotient. In some cases, you might encounter remainders when a number doesn’t divide evenly. Even with a remainder, the quotient is still the primary result, and the remainder is noted separately. This entire process can be explained in simple terms with free consultation at WHAT.EDU.VN.
4. Terms Related to Quotient
Besides the quotient, understanding other terms involved in division is essential. Consider a scenario: a chocolate bar with 12 pieces needs to be shared equally between two friends. Each friend receives 6 pieces, with nothing left over. In this case, the division statement is 12 ÷ 2 = 6. Let’s break down these numbers.
| Terms | Descriptions | Values |
|---|---|---|
| Dividend | The total number to be shared. | 12 |
| Divisor | The number of equal groups to be made. | 2 |
| Quotient | The number in each group. | 6 |
| Remainder | The piece left that is not part of any group. | 0 |
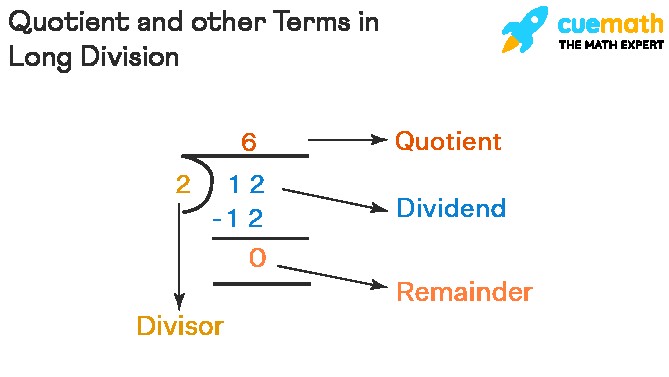
The figure below illustrates these terms in a long division format, showing how they relate to each other in the division process.
5. Quotient and Remainder
When a number doesn’t divide evenly, you’re left with a remainder. The quotient is the whole number result of the division, while the remainder is what’s left over. To calculate this, divide the dividend by the divisor using the formula:
Quotient = Dividend ÷ Divisor
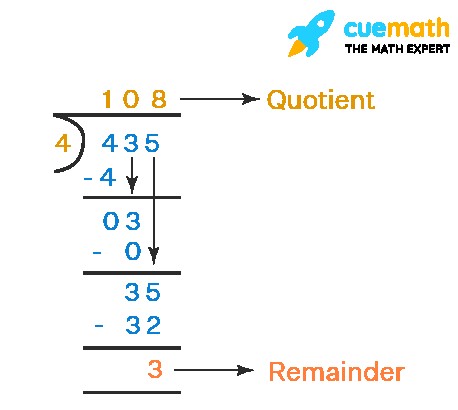
For example, let’s divide 435 ÷ 4. Here, 435 is the dividend, and 4 is the divisor.
Here are the steps to understand the division process and find the quotient and the remainder:
- Step 1: Take the first digit of the dividend. If this digit is greater than or equal to the divisor, then divide it by the divisor and write the answer on top as a part of the quotient. Multiply this number with the divisor and write the product below the first digit of the dividend. Subtract the result from the digit and write it below that number. Here, the first digit is 4 and it is equal to the divisor. So, 4 ÷ 4 = 1 is written on top of the bar. The product of 4 × 1 = 4 is subtracted from the digit and 0 is written below. Now, bring down the next number of the dividend which is 3 and place it next to 0.
- Step 2: We can see that we have 3 as the result of step 1. Repeat the same step of checking if this number is greater or smaller than the divisor. Since 3 is less than 4, we cannot divide this number. Hence, we write a 0 on the top and write the product of 4 × 0 = 0 below the 3, then subtract 3 – 0 = 3. The next step is to bring down the next number from the dividend and place it beside 3. This makes it 35. As 35 > 4, we can divide this number by 4. After writing 8 on top, we write the product of 4 × 8 = 32 below 35 as shown. Subtract 35 – 32 = 3. Now, this 3 is smaller than the divisor 4 and there is no number left to be brought down from the dividend. This means we will leave 3 as the remainder and complete the division. Therefore, 3 is known as the remainder and 108 is called the quotient.
Verification of the Division Result
To ensure accuracy, you can verify your division result using the formula:
Dividend = (Divisor × Quotient) + Remainder
Using our previous example, where the dividend is 435, the divisor is 4, the quotient is 108, and the remainder is 3, we can verify:
435 = (4 × 108) + 3
This confirms that our division is correct.
6. Estimating Quotient
Estimating the quotient involves approximating the result by rounding the divisor and dividend to numbers that are easier to compute. This method is useful for quickly finding an approximate answer without performing exact calculations. Let’s illustrate with an example: 64 ÷ 22
- Step 1: We need to divide 64 ÷ 22. Here, 64 is the dividend and the divisor is 22 and we need to estimate the quotient.
- Step 2: We first need to round off the dividend 64 to the nearest tens because the last place value here is tens. After checking the digit at ones place, it will be rounded down to 60 because the digit at ones place (that is 4) is less than 5. Similarly, the divisor will also be rounded off to the nearest tens because in 22, the last place value is tens. So we need to check the digit in ones place (that is 2) which is less than 5. Therefore, 22 will be rounded down to 20.
- Step 3: Now, we have rounded the given numbers and it has become 60 ÷ 20. We can simply divide it and we get 3 as the estimated quotient.
- Step 4: Another method to estimate the quotient is to eliminate the least number of zeros in the estimated (rounded) divisor and the estimated (rounded) dividend. So, in this case, after eliminating the least number of zeros, 60 ÷ 20 becomes 6 ÷ 2 and we get the quotient as 3. So, we got the same estimated quotient by both the methods.
Example: Estimate the quotient of 825 divided by 24.
Solution: In the given question, we need to divide 825 ÷ 24.
- Step 1: We need to round off the divisor and the dividend. Since in 825, the last place value is hundreds, we need to round it off to the nearest hundreds. For this, we need to check the digit on tens place. Here, it is 2, which is less than 5. So 825 will be rounded down to 800. Similarly, since in 24, the last place value is tens, we need to round it off to the nearest tens. For this, we need to check the digit on ones place. Here, it is 4, which is less than 5. So 24 will be rounded down to 20.
- Step 2: Now, we need to divide 800 ÷ 20, which can be simply divided and we get the estimated quotient as 40.
7. Examples on Quotient
7.1. Example 1
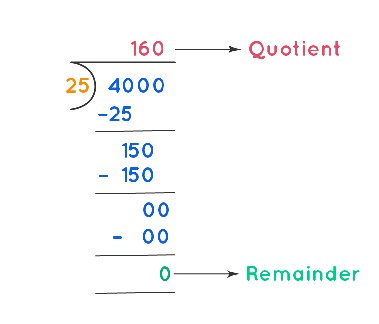
$4000 is distributed among 25 workers for the work completed by them at a construction site. Calculate the amount given to each worker.
Solution:
The total amount to be distributed = $4000. The number of workers = 25. We need to calculate the amount given to each worker. To do so, we will divide 4000 by 25 using the long division method and find the quotient.
The quotient that we get is 160. Therefore, the amount given to each worker is $160.
7.2. Example 2
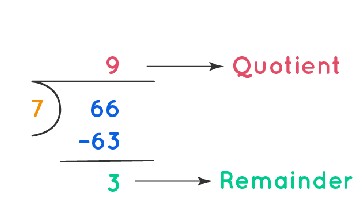
Divide 66 ÷ 7 and find the quotient and remainder.
Solution:
We will use the long division method to find the quotient.
After dividing 66 by 7 we get 9 as the quotient and 3 as the remainder.
7.3. Example 3
State true or false:
a.) Quotient is the final answer that we get when we divide a number.
b.) When we divide a number and if it does not get divided completely, we are left with a remainder.
Solution:
a.) True, quotient is the final answer that we get when we divide a number.
b.) True, when we divide a number and if it does not get divided completely, we are left with a remainder.
8. Why Understanding the Quotient is Important?
Understanding the quotient is crucial for several reasons:
- Everyday Problem Solving: Knowing how to find a quotient helps in everyday situations like splitting bills, sharing resources, or calculating averages.
- Building Block for Higher Math: The concept of the quotient is fundamental to more complex mathematical operations such as algebra, calculus, and statistics.
- Financial Literacy: Understanding quotients can aid in financial planning, budgeting, and investment calculations.
9. Common Mistakes to Avoid When Calculating Quotients
- Incorrect Division: Ensure the division is performed accurately, paying attention to place values.
- Forgetting the Remainder: Always account for the remainder when it exists, as it can be significant in certain contexts.
- Misunderstanding the Terms: Clearly differentiate between the dividend, divisor, quotient, and remainder to avoid confusion.
10. Tips for Mastering Quotients
- Practice Regularly: Consistent practice with division problems will improve your proficiency.
- Use Visual Aids: Employ diagrams and visual representations to better understand the concept.
- Apply Real-Life Scenarios: Relate division problems to real-world situations to make the learning more engaging.
- Seek Help: If you’re struggling, don’t hesitate to ask for help from teachers, tutors, or online resources.
11. Practice Questions on Quotient
(Practice questions will be added here to allow readers to test their understanding)
12. FAQs on Quotient
12.1. What is Quotient in Math?
The quotient is the result you obtain when dividing one number by another. For example, if you divide 63 ÷ 9, you get 7. In this case, 7 is the quotient. It’s important to note that the quotient can be larger or smaller than the divisor but is always smaller than the dividend.
12.2. How to Find the Quotient in Division?
You find the quotient after completing the division process. This means that when a divisor divides a dividend, the resulting answer is the quotient. Alternatively, you can use the formula: Dividend ÷ Divisor = Quotient. A simple example is 12 ÷ 4 = 3. Here, 12 is the dividend, 4 is the divisor, and 3 is the quotient.
12.3. Is Quotient Always a Whole Number?
No, the quotient is not always a whole number. It can be a whole number or a decimal number. In perfect divisions like 16 ÷ 2 = 8, the quotient is a whole number. However, when you’re left with a remainder, you can continue dividing by placing a decimal in the quotient, resulting in a decimal number. For instance, if you divide 16 ÷ 5, you get 3.2 as the quotient, which is a decimal number.
12.4. What is the Difference Between Quotient and Remainder?
The quotient is the result obtained when you divide a number, whereas the remainder is the amount left over after the division is complete. The remainder is what remains after the division process. For example, if you need to distribute 7 balls equally between 2 children, each child gets 3 balls, and you have 1 ball left over. This remaining 1 ball is the remainder. Mathematically, 7 cannot be completely divided by 2, leaving 1 as the remainder. In perfect divisions, the remainder is zero, and the quotient is a whole number.
12.5. How Can we Verify the Quotient in Division?
Division is also known as inverse multiplication. You can verify the quotient using the formula:
Dividend = (Divisor × Quotient) + Remainder
This means that if you multiply the divisor by the quotient and add the remainder, you should get the dividend. If the numbers satisfy this equation, your answer is correct; otherwise, you need to recheck your division.
12.6. How to Find the Quotient When the Remainder and Divisor is given?
If the remainder, divisor, and dividend are given, you can easily find the quotient by substituting the values into the formula: Dividend = (Divisor × Quotient) + Remainder. After substituting the known values, you can solve for the quotient.
12.7. What is the Quotient of 21 Divided by 7?
When 21 is divided by 7, the quotient is 3. Here, 21 is the dividend, 7 is the divisor, and 3 is the quotient.
12.8. What is the Difference Between Quotient and Product?
‘Quotient’ is the result of division, while ‘product’ is the result of multiplication. The quotient is smaller than the dividend and the divisor, while the product is larger than the numbers being multiplied.
12.9. How to Estimate the Quotient?
To estimate the quotient, first round off the divisor and the dividend, and then divide them. For example, if you need to estimate the quotient for 84 ÷ 18, round 84 down to 80 and 18 up to 20. So, you get 80 ÷ 20, which equals 4. Therefore, the estimated quotient is 4.
In conclusion, mastering the concept of the quotient is essential for building a strong foundation in mathematics. Whether you’re solving everyday problems or tackling complex equations, understanding how to find and estimate quotients will prove invaluable.
Do you have more questions about quotients or other math topics? Visit WHAT.EDU.VN today and get your questions answered for free! Our platform offers a seamless way to ask questions and receive prompt, accurate answers from knowledgeable experts. Don’t let math challenges hold you back. Contact us at 888 Question City Plaza, Seattle, WA 98101, United States, or reach out via WhatsApp at +1 (206) 555-7890. Visit our website at what.edu.vn for more information. We’re here to help you succeed!