What Is Slope Intercept Form: Your Ultimate Guide?

Are you struggling with linear equations and need a clear understanding of What Is Slope Intercept Form? At what.edu.vn, we provide simple, accessible explanations to help you grasp this essential concept. Slope intercept form is a specific way to write linear equations that makes identifying the slope and y-intercept straightforward. Dive in to discover how this form simplifies graphing and problem-solving, enhancing your understanding of linear functions, linear equations, and coordinate geometry.

1. What is Slope Intercept Form?

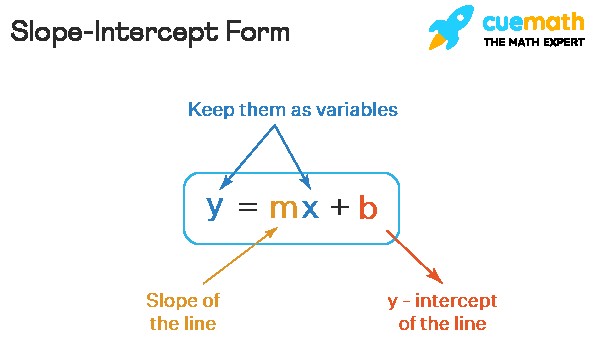
The slope-intercept form is a way to represent the equation of a straight line on a coordinate plane. Understanding this form is crucial because it directly reveals two key properties of the line: its slope and its y-intercept. The equation is written as:

y = mx + b

Where:

y is the dependent variable, representing the vertical coordinate.
x is the independent variable, representing the horizontal coordinate.
m is the slope of the line, indicating its steepness and direction.
b is the y-intercept, the point where the line crosses the y-axis (where x = 0).

Slope intercept form of a straight line

1.1. Why is Slope Intercept Form Important?

Slope-intercept form is important for several reasons:

Ease of Graphing: It makes it simple to graph a line because you can immediately identify the y-intercept (starting point) and use the slope to find other points on the line.
Problem Solving: It simplifies many algebra problems involving linear equations.
Real-World Applications: It helps model real-world scenarios, such as calculating costs, distances, or rates.

1.2. Real-World Examples

Consider these examples:

Cost Function: Suppose a taxi charges a flat fee of $3 plus $2 per mile. The equation would be y = 2x + 3, where ‘y’ is the total cost and ‘x’ is the number of miles.
Savings Plan: If you start with $50 in savings and add $25 each week, the equation is y = 25x + 50, where ‘y’ is the total savings and ‘x’ is the number of weeks.

1.3. Common Mistakes to Avoid

Confusing Slope and Intercept: Ensure you correctly identify which number is the slope (m) and which is the y-intercept (b).
Incorrectly Applying the Slope: Remember that the slope is “rise over run.” If the slope is negative, the line goes downward from left to right.
Ignoring the Sign: Pay attention to the signs of ‘m’ and ‘b’. A negative slope means the line decreases, and a negative y-intercept means the line crosses the y-axis below the origin.

2. Understanding Slope

The slope, denoted as ‘m’ in the slope-intercept form (y = mx + b), measures the steepness and direction of a line. It is formally defined as the “rise over run,” representing the change in ‘y’ for every unit change in ‘x’.

2.1. Calculating Slope

To calculate the slope (m) between two points (x₁, y₁) and (x₂, y₂), use the formula:

m = (y₂ – y₁) / (x₂ – x₁)

This formula calculates the change in ‘y’ divided by the change in ‘x’, giving you the rate at which the line is increasing or decreasing.

2.2. Interpreting the Slope Value

Positive Slope (m > 0): The line rises from left to right. This means as ‘x’ increases, ‘y’ also increases.
Negative Slope (m < 0): The line falls from left to right. This means as ‘x’ increases, ‘y’ decreases.
Zero Slope (m = 0): The line is horizontal. There is no change in ‘y’ as ‘x’ changes.
Undefined Slope: The line is vertical. The change in ‘x’ is zero, leading to division by zero in the slope formula.

2.3. Examples of Slope Calculation

Example 1: Points (1, 2) and (3, 6)
- m = (6 – 2) / (3 – 1) = 4 / 2 = 2
- The slope is 2, meaning for every 1 unit increase in ‘x’, ‘y’ increases by 2.
Example 2: Points (2, 5) and (4, 1)
- m = (1 – 5) / (4 – 2) = -4 / 2 = -2
- The slope is -2, meaning for every 1 unit increase in ‘x’, ‘y’ decreases by 2.
Example 3: Points (1, 3) and (5, 3)
- m = (3 – 3) / (5 – 1) = 0 / 4 = 0
- The slope is 0, indicating a horizontal line.

2.4. Special Cases

Parallel Lines: Parallel lines have the same slope. If line 1 has a slope of m₁, and line 2 has a slope of m₂, then for the lines to be parallel, m₁ = m₂.
Perpendicular Lines: Perpendicular lines have slopes that are negative reciprocals of each other. If line 1 has a slope of m₁, and line 2 has a slope of m₂, then for the lines to be perpendicular, m₁ = -1 / m₂ or m₁ * m₂ = -1.

Understanding the concept of slope is fundamental in analyzing linear relationships. Whether you are solving mathematical problems or interpreting real-world data, the slope provides valuable insights into the behavior of a line.

3. Understanding the Y-Intercept

The y-intercept is the point where the line intersects the y-axis. In the slope-intercept form of a linear equation (y = mx + b), the y-intercept is represented by ‘b’. It is the value of ‘y’ when ‘x’ is zero.

3.1. Identifying the Y-Intercept

Definition: The y-intercept is the point (0, b) on the coordinate plane.
Graphical Representation: It is where the line crosses the vertical y-axis.

3.2. Importance of the Y-Intercept

Starting Point: The y-intercept serves as the starting point when graphing a line. You begin by plotting this point on the y-axis.
Real-World Meaning: In practical scenarios, the y-intercept often represents an initial value or a fixed cost. For example, in a cost equation, it might be the base fee before any additional charges.

3.3. Examples of Identifying the Y-Intercept

Equation: y = 3x + 4
- The y-intercept is 4.
- This means the line crosses the y-axis at the point (0, 4).
Equation: y = -2x – 1
- The y-intercept is -1.
- This means the line crosses the y-axis at the point (0, -1).
Equation: y = (1/2)x + 5
- The y-intercept is 5.
- This means the line crosses the y-axis at the point (0, 5).

3.4. Finding the Y-Intercept from a Graph

Locate the Y-Axis: Find the vertical y-axis on the graph.
Identify the Intersection: Determine where the line intersects the y-axis.
Read the Y-Value: The y-value at the point of intersection is the y-intercept.

3.5. Finding the Y-Intercept from Two Points

If you have two points (x₁, y₁) and (x₂, y₂), follow these steps to find the y-intercept:

Calculate the Slope: Use the slope formula m = (y₂ – y₁) / (x₂ – x₁).
Use Point-Slope Form: Choose one of the points and use the point-slope form of a linear equation: y – y₁ = m(x – x₁).
Convert to Slope-Intercept Form: Rewrite the equation in the form y = mx + b to find the y-intercept ‘b’.

3.6. Example: Finding Y-Intercept from Points (2, 3) and (4, 7)

Calculate the Slope:
- m = (7 – 3) / (4 – 2) = 4 / 2 = 2
Use Point-Slope Form:
- Using point (2, 3): y – 3 = 2(x – 2)
Convert to Slope-Intercept Form:
- y – 3 = 2x – 4
- y = 2x – 4 + 3
- y = 2x – 1
- The y-intercept is -1.

Understanding the y-intercept is essential for both graphing and interpreting linear equations. It provides a concrete starting point and often carries significant real-world meaning.

4. How to Write an Equation in Slope Intercept Form

Writing an equation in slope-intercept form (y = mx + b) involves identifying or calculating the slope (m) and the y-intercept (b). Here’s a step-by-step guide with examples to help you through the process.

4.1. Steps to Write an Equation in Slope-Intercept Form

Identify the Slope (m):
- If given two points, use the slope formula: m = (y₂ – y₁) / (x₂ – x₁).
- If given the angle of inclination (θ), use: m = tan(θ).
- If the line is parallel to another line, it has the same slope.
- If the line is perpendicular to another line, its slope is the negative reciprocal.
Identify the Y-Intercept (b):
- If given, it’s the point where the line crosses the y-axis (x = 0).
- If not given, use one point (x₁, y₁) on the line and the slope (m) in the point-slope form: y – y₁ = m(x – x₁). Solve for y to get the slope-intercept form.
Write the Equation:
- Substitute the values of ‘m’ and ‘b’ into the slope-intercept form: y = mx + b.

4.2. Example 1: Given Slope and Y-Intercept

Slope (m) = 3
Y-Intercept (b) = -2

Write the equation: y = 3x – 2

4.3. Example 2: Given Two Points (1, 7) and (3, 13)

Calculate the Slope:
- m = (13 – 7) / (3 – 1) = 6 / 2 = 3
Identify the Y-Intercept:
- Use the point-slope form with point (1, 7): y – 7 = 3(x – 1)
- Solve for y: y – 7 = 3x – 3
- y = 3x – 3 + 7
- y = 3x + 4
- The y-intercept (b) = 4
Write the Equation: y = 3x + 4

4.4. Example 3: Given a Point and a Parallel Line

Point: (2, 1)
Parallel Line: y = 2x + 3

Identify the Slope:
- The slope of the parallel line is 2, so the slope of the line we want to find is also 2.
Identify the Y-Intercept:
- Use the point-slope form with point (2, 1): y – 1 = 2(x – 2)
- Solve for y: y – 1 = 2x – 4
- y = 2x – 4 + 1
- y = 2x – 3
- The y-intercept (b) = -3
Write the Equation: y = 2x – 3

4.5. Example 4: Given a Point and a Perpendicular Line

Point: (3, 2)
Perpendicular Line: y = (-1/2)x + 1

Identify the Slope:
- The slope of the perpendicular line is -1/2, so the slope of the line we want to find is the negative reciprocal: m = 2
Identify the Y-Intercept:
- Use the point-slope form with point (3, 2): y – 2 = 2(x – 3)
- Solve for y: y – 2 = 2x – 6
- y = 2x – 6 + 2
- y = 2x – 4
- The y-intercept (b) = -4
Write the Equation: y = 2x – 4

4.6. Common Mistakes to Avoid

Incorrectly Calculating Slope: Double-check your calculations when using the slope formula.
Using the Wrong Point: Ensure you correctly substitute the coordinates when using the point-slope form.
Forgetting to Solve for Y: Always solve the equation for y to get it into slope-intercept form.

By following these steps and practicing with examples, you can confidently write equations in slope-intercept form. This skill is essential for solving various problems in algebra and understanding linear relationships.

5. Graphing Linear Equations Using Slope Intercept Form

Graphing linear equations using slope-intercept form (y = mx + b) is a straightforward process. This method allows you to quickly visualize the line by using the y-intercept as a starting point and the slope to find additional points.

5.1. Steps to Graph a Line Using Slope-Intercept Form

Identify the Y-Intercept (b):
- The y-intercept is the point where the line crosses the y-axis. Plot this point (0, b) on the graph.
Identify the Slope (m):
- The slope represents the rise over run. Write the slope as a fraction (if it’s not already).
- m = rise / run
Use the Slope to Find Additional Points:
- From the y-intercept, use the rise and run to find another point on the line.
  - Rise: Move vertically by the number of units indicated by the numerator of the slope.
  - Run: Move horizontally by the number of units indicated by the denominator of the slope.
- Plot this new point.
Draw the Line:
- Draw a straight line through the y-intercept and the new point you found.
- Extend the line in both directions to fill the graph.

5.2. Example 1: Graphing y = 2x + 3

Identify the Y-Intercept:
- b = 3
- Plot the point (0, 3) on the y-axis.
Identify the Slope:
- m = 2
- Write it as a fraction: m = 2 / 1
- Rise = 2, Run = 1
Use the Slope to Find Additional Points:
- From the y-intercept (0, 3), move up 2 units (rise) and right 1 unit (run) to find the next point (1, 5).
- Plot the point (1, 5).
Draw the Line:
- Draw a straight line through the points (0, 3) and (1, 5).

5.3. Example 2: Graphing y = (-1/3)x – 2

Identify the Y-Intercept:
- b = -2
- Plot the point (0, -2) on the y-axis.
Identify the Slope:
- m = -1/3
- Rise = -1, Run = 3
Use the Slope to Find Additional Points:
- From the y-intercept (0, -2), move down 1 unit (rise) and right 3 units (run) to find the next point (3, -3).
- Plot the point (3, -3).
Draw the Line:
- Draw a straight line through the points (0, -2) and (3, -3).

5.4. Example 3: Graphing y = 3x – 1

Identify the Y-Intercept:
- b = -1
- Plot the point (0, -1) on the y-axis.
Identify the Slope:
- m = 3
- Write it as a fraction: m = 3 / 1
- Rise = 3, Run = 1
Use the Slope to Find Additional Points:
- From the y-intercept (0, -1), move up 3 units (rise) and right 1 unit (run) to find the next point (1, 2).
- Plot the point (1, 2).
Draw the Line:
- Draw a straight line through the points (0, -1) and (1, 2).

5.5. Common Mistakes to Avoid

Plotting the Y-Intercept Incorrectly:
- Make sure to plot the y-intercept on the y-axis (0, b).
Misinterpreting the Slope:
- Remember that the slope is rise over run. A negative slope means you move down (negative rise) and right (positive run).
Reversing Rise and Run:
- Always move vertically according to the rise and horizontally according to the run.

By following these steps, you can easily graph linear equations using the slope-intercept form. This method provides a clear and visual way to understand linear relationships.

6. Converting Equations to Slope Intercept Form

Converting equations to slope-intercept form (y = mx + b) is a useful skill for analyzing and graphing linear equations. This form makes it easy to identify the slope and y-intercept, which simplifies many algebraic tasks.

6.1. Steps to Convert Equations to Slope-Intercept Form

Start with the Given Equation:
- Begin with the equation in any form (e.g., standard form, point-slope form, etc.).
Isolate ‘y’ on One Side:
- Use algebraic operations (addition, subtraction, multiplication, division) to isolate ‘y’ on one side of the equation.
Simplify the Equation:
- Combine like terms and simplify the equation to the form y = mx + b.

6.2. Example 1: Converting from Standard Form (Ax + By = C)

Given Equation: 2x + 3y = 6

Isolate ‘y’:
- Subtract 2x from both sides: 3y = -2x + 6
Divide by 3:
- Divide all terms by 3: y = (-2/3)x + 2
Slope-Intercept Form:
- y = (-2/3)x + 2
- Slope (m) = -2/3
- Y-Intercept (b) = 2

6.3. Example 2: Converting from Point-Slope Form (y – y₁ = m(x – x₁))

Given Equation: y – 4 = 2(x – 1)

Distribute:
- Distribute the 2: y – 4 = 2x – 2
Isolate ‘y’:
- Add 4 to both sides: y = 2x – 2 + 4
Simplify:
- y = 2x + 2
Slope-Intercept Form:
- y = 2x + 2
- Slope (m) = 2
- Y-Intercept (b) = 2

6.4. Example 3: Converting a Linear Equation with Fractions

Given Equation: (1/2)x – (1/4)y = 1

Multiply to Eliminate Fractions:
- Multiply all terms by 4 to eliminate fractions: 2x – y = 4
Isolate ‘y’:
- Subtract 2x from both sides: -y = -2x + 4
Multiply by -1:
- Multiply all terms by -1 to solve for y: y = 2x – 4
Slope-Intercept Form:
- y = 2x – 4
- Slope (m) = 2
- Y-Intercept (b) = -4

6.5. Common Mistakes to Avoid

Incorrectly Distributing:
- Ensure you distribute correctly when removing parentheses.
Forgetting to Divide All Terms:
- When dividing to isolate ‘y’, divide all terms in the equation.
Sign Errors:
- Pay close attention to signs when adding, subtracting, multiplying, or dividing.

By mastering these steps, you can easily convert linear equations into slope-intercept form, allowing you to quickly identify and analyze the properties of the line.

7. Applications of Slope Intercept Form in Real Life

The slope-intercept form (y = mx + b) is not just a mathematical concept; it has numerous practical applications in real life. Understanding how to use this form can help you model and solve problems in various fields.

7.1. Business and Finance

Cost Analysis:
- Scenario: A company has a fixed cost (e.g., rent) and a variable cost per unit produced.
- Equation: Total Cost (y) = (Variable Cost per Unit × Number of Units) + Fixed Cost
- Example: If a company has a fixed cost of $1000 and a variable cost of $5 per unit, the equation is y = 5x + 1000.
Sales and Revenue:
- Scenario: Predicting sales based on a linear growth model.
- Equation: Total Sales (y) = (Sales Increase per Period × Number of Periods) + Initial Sales
- Example: If a store starts with $500 in sales and increases by $50 each week, the equation is y = 50x + 500.
Depreciation:
- Scenario: Calculating the depreciation of an asset over time.
- Equation: Asset Value (y) = (Depreciation per Year × Number of Years) + Initial Value
- Example: If a car is bought for $20,000 and depreciates $2000 each year, the equation is y = -2000x + 20000.

7.2. Science and Engineering

Physics:
- Scenario: Describing the motion of an object with constant velocity.
- Equation: Distance (y) = (Velocity × Time) + Initial Distance
- Example: If a car starts 10 miles away and travels at 60 mph, the equation is y = 60x + 10.
Chemistry:
- Scenario: Modeling linear relationships between temperature and reaction rates.
- Equation: Reaction Rate (y) = (Rate Change per Degree × Temperature) + Initial Rate
Environmental Science:
- Scenario: Modeling the change in pollution levels over time.
- Equation: Pollution Level (y) = (Change in Pollution per Year × Number of Years) + Initial Pollution Level

7.3. Everyday Life

Budgeting:
- Scenario: Managing a budget with fixed expenses and variable spending.
- Equation: Total Spending (y) = (Spending per Unit Time × Number of Units of Time) + Fixed Expenses
- Example: If you have fixed expenses of $500 and spend $20 per day, the equation is y = 20x + 500.
Travel:
- Scenario: Calculating the total cost of a taxi ride.
- Equation: Total Cost (y) = (Cost per Mile × Number of Miles) + Initial Fee
- Example: If a taxi charges $2 per mile plus a $3 initial fee, the equation is y = 2x + 3.
Cooking:
- Scenario: Adjusting recipe quantities.
- Equation: Total Quantity (y) = (Ingredient per Serving × Number of Servings) + Base Quantity

7.4. Example: Fitness and Exercise

Scenario: Tracking progress in a fitness plan.
Equation: Weight Loss (y) = (Weight Loss per Week × Number of Weeks) + Starting Weight
Example: If you start at 200 lbs and lose 2 lbs per week, the equation is y = -2x + 200.

7.5. Benefits of Using Slope-Intercept Form

Prediction: Easily predict future values based on current trends.
Analysis: Understand the rate of change and initial conditions in a given scenario.
Decision Making: Make informed decisions based on mathematical models.

By understanding these applications, you can see how the slope-intercept form is a powerful tool for modeling and solving real-world problems.

8. Advantages and Disadvantages of Slope Intercept Form

Slope-intercept form (y = mx + b) is a widely used method for representing linear equations, but it has its strengths and weaknesses. Understanding these advantages and disadvantages can help you decide when and how to use it effectively.

8.1. Advantages of Slope-Intercept Form

Simplicity and Clarity:
- Advantage: The form is straightforward and easy to understand. The slope (m) and y-intercept (b) are immediately visible, making it simple to interpret the equation.
- Example: In the equation y = 2x + 3, it’s clear that the slope is 2 and the y-intercept is 3.
Ease of Graphing:
- Advantage: It simplifies graphing linear equations. You can plot the y-intercept as a starting point and use the slope to find additional points.
- Example: To graph y = -x + 1, start at the point (0, 1) and use the slope of -1 to find other points.
Quick Analysis:
- Advantage: The slope and y-intercept provide quick insights into the line’s behavior, such as its direction (increasing or decreasing) and starting point on the y-axis.
- Example: A line with a negative slope (e.g., y = -3x + 5) is decreasing, while a line with a positive slope (e.g., y = 4x – 2) is increasing.
Real-World Applications:
- Advantage: It is useful for modeling real-world situations where there is a constant rate of change and an initial value.
- Example: Modeling a cost function with a fixed cost and a variable cost per unit.
Direct Comparison:
- Advantage: It allows for easy comparison of different linear equations. By looking at the slopes, you can quickly determine if lines are parallel or perpendicular.
- Example: If two lines have the same slope (e.g., y = 2x + 3 and y = 2x – 1), they are parallel.

8.2. Disadvantages of Slope-Intercept Form

Not Suitable for Vertical Lines:
- Disadvantage: Slope-intercept form cannot represent vertical lines because the slope of a vertical line is undefined.
- Explanation: Vertical lines have the equation x = c, which cannot be written in the form y = mx + b.
Requires Solving for ‘y’:
- Disadvantage: Converting equations from other forms (like standard form) requires isolating ‘y’, which can be time-consuming and prone to errors.
- Example: Converting 2x + 3y = 6 to slope-intercept form involves multiple steps.
Less Convenient for Some Problems:
- Disadvantage: It may not be the most convenient form for solving certain types of problems, such as finding the equation of a line given two points, where point-slope form might be more efficient.
- Explanation: Point-slope form (y – y₁ = m(x – x₁)) directly uses the given points without needing to find the y-intercept first.
Limited to Linear Equations:
- Disadvantage: It only applies to linear equations and cannot be used for non-linear relationships.
- Example: Quadratic, exponential, and trigonometric functions cannot be represented in slope-intercept form.
Potential for Misinterpretation:
- Disadvantage: If not careful, it’s easy to misinterpret the slope and y-intercept, especially with negative values or fractions.
- Example: Confusing the slope and y-intercept in the equation y = (-1/2)x + 4.

8.3. When to Use Slope-Intercept Form

Use When:
- You need to quickly graph a linear equation.
- You want to easily identify the slope and y-intercept.
- You are modeling a real-world situation with a constant rate of change and an initial value.
Avoid When:
- You are dealing with vertical lines.
- You need to quickly find the equation of a line given two points.
- You are working with non-linear equations.

Understanding these advantages and disadvantages allows you to make informed decisions about when to use slope-intercept form, ensuring you choose the most efficient and effective method for your specific needs.

9. Common Mistakes When Using Slope Intercept Form

Using slope-intercept form (y = mx + b) is generally straightforward, but there are several common mistakes that students and others often make. Being aware of these mistakes can help you avoid them and ensure accurate results.

9.1. Confusing Slope and Y-Intercept

Mistake: Incorrectly identifying which number is the slope (m) and which is the y-intercept (b).
Correct Understanding: The slope (m) is the coefficient of x, and the y-intercept (b) is the constant term.
Example: In the equation y = 3x + 2, the slope is 3, and the y-intercept is 2, not the other way around.

9.2. Sign Errors

Mistake: Ignoring or mishandling negative signs.
Correct Understanding: A negative slope indicates a decreasing line, and a negative y-intercept means the line crosses the y-axis below the origin.
Example: In the equation y = -2x – 1, the slope is -2 (line decreases), and the y-intercept is -1 (crosses y-axis at (0, -1)).

9.3. Misinterpreting Zero Slope

Mistake: Thinking a zero slope means the line is vertical or not understanding that it’s a horizontal line.
Correct Understanding: A zero slope (m = 0) means the line is horizontal and has the equation y = b.
Example: The equation y = 5 represents a horizontal line passing through (0, 5).

9.4. Undefined Slope Errors

Mistake: Trying to apply slope-intercept form to vertical lines.
Correct Understanding: Vertical lines have an undefined slope and cannot be written in slope-intercept form. They are represented by the equation x = c, where c is a constant.
Example: The equation x = 3 represents a vertical line passing through (3, 0).

9.5. Incorrectly Calculating Slope

Mistake: Errors in using the slope formula (m = (y₂ – y₁) / (x₂ – x₁)).
Correct Understanding: Ensure you subtract the y-coordinates and x-coordinates in the same order.
Example: Given points (1, 3) and (4, 9), the slope is (9 – 3) / (4 – 1) = 6 / 3 = 2.

9.6. Reversing Rise and Run

Mistake: Swapping the rise and run when using the slope to find additional points on the line.
Correct Understanding: The slope is rise over run. Move vertically according to the rise (numerator) and horizontally according to the run (denominator).
Example: If the slope is 3/4, move up 3 units and right 4 units.

9.7. Not Simplifying Equations

Mistake: Leaving equations in a non-simplified form, making it hard to identify the slope and y-intercept.
Correct Understanding: Simplify the equation to the form y = mx + b by isolating y.
Example: Convert 2x + y = 5 to y = -2x + 5 to clearly see the slope and y-intercept.

9.8. Incorrectly Plotting Points

Mistake: Misplotting the y-intercept or other points on the graph.
Correct Understanding: The y-intercept is plotted on the y-axis (0, b). Use