What Is The Area? It’s a fundamental concept in geometry and has practical applications in everyday life. At WHAT.EDU.VN, we’re committed to providing clear, concise answers to your questions. Let’s explore the definition, formulas, and various aspects of area, ensuring you have a solid understanding of this important topic. Learn about area calculation, surface area and space it covers, empowering you with knowledge for academic success and real-world applications.
1. Understanding the Basics of “What is the Area?”
The area is the amount of two-dimensional space a shape occupies. It’s a measure of the surface within a set of boundaries. Understanding this concept is crucial for various applications, from calculating the size of a room to determining the amount of material needed for a project.
1.1 What is the Area: Defining the Concept
Area, in its simplest form, is the measure of the surface of a two-dimensional shape. Think of it as the amount of paint you would need to cover a flat surface once. This concept is fundamental to geometry and has practical applications in fields like architecture, engineering, and design.
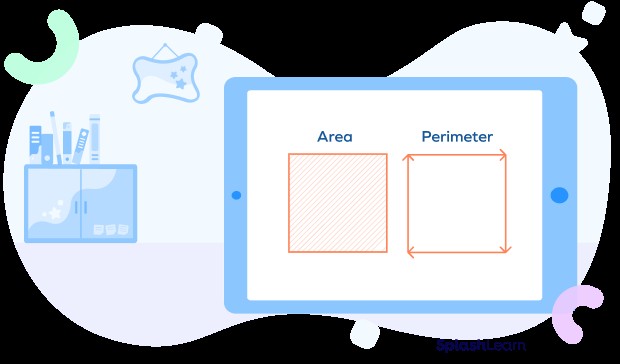
1.2 Area vs. Perimeter: What’s the Difference?
While both area and perimeter relate to shapes, they measure different aspects. Perimeter is the total distance around the outside of a shape, like the length of a fence needed to enclose a yard. Area, on the other hand, measures the space enclosed by that fence.
| Area | Perimeter |
|---|---|
| The space occupied by a closed plane in a two-dimensional shape is called area. | Perimeter is the measure of the length of the outer boundary of a closed shape. |
| Area is measured in squared units. | Perimeter is measured in units. |
| Example: Area of tiling the floor | Example: Perimeter of fencing the garden |
1.3 Area vs. Volume: Clarifying the Dimensions
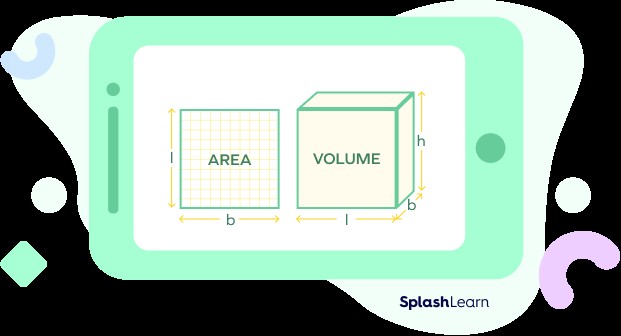
Area deals with two-dimensional shapes, while volume deals with three-dimensional objects. Imagine a square (2D) and a cube (3D). Area is the space inside the square, while volume is the space inside the cube.
| Area | Volume |
|---|---|
| Area is defined for 2-dimensional space. | Volume is defined for 3-dimensional space. |
| The space occupied by a closed plane in a 2-dimensional shape is called area. | The space occupied by a 3-dimensional figure is known as volume. |
| Example: Area of tiling the floor | Example: Volume of the room |
2. Why is Understanding “What is the Area?” Important?
Understanding area is essential for a multitude of reasons. It helps in practical tasks like home improvement, gardening, and construction. It’s also a fundamental concept in mathematics and science, crucial for problem-solving and analytical thinking.
2.1 Practical Applications in Daily Life
From calculating the amount of carpet needed for a room to determining the size of a garden, area calculations are used in everyday situations. It helps in making informed decisions and avoiding wastage.
2.2 Importance in Mathematics and Geometry
Area is a building block for more advanced mathematical concepts. It forms the basis for understanding volume, surface area, and integral calculus. A solid grasp of area is crucial for success in higher-level mathematics.
2.3 Applications in Various Fields
Architecture, engineering, design, and even agriculture rely heavily on area calculations. Architects use it to design buildings, engineers use it to calculate stress on surfaces, and farmers use it to determine the yield of their crops.
3. Formulas for Calculating “What is the Area?”
The formula for calculating area varies depending on the shape. Here are some common formulas:
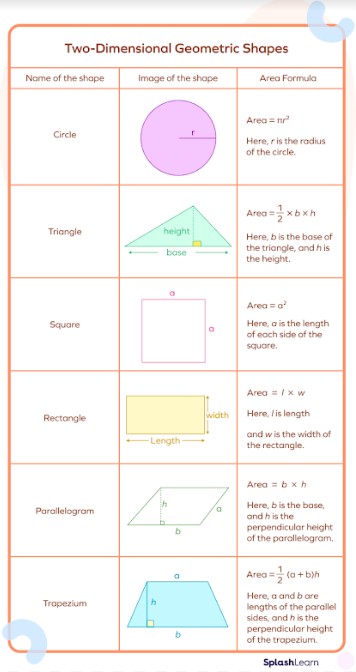
- Square: Area = side x side
- Rectangle: Area = length x width
- Triangle: Area = 1/2 x base x height
- Circle: Area = π x radius²
3.1 Area of a Square: A Simple Calculation
The area of a square is found by multiplying the length of one side by itself. If a square has a side of 5 cm, its area is 5 cm x 5 cm = 25 cm².
3.2 Area of a Rectangle: Length Times Width
To find the area of a rectangle, multiply its length by its width. For example, a rectangle with a length of 10 cm and a width of 4 cm has an area of 10 cm x 4 cm = 40 cm².
3.3 Area of a Triangle: Half Base Times Height
The area of a triangle is calculated by multiplying half of its base by its height. If a triangle has a base of 8 cm and a height of 6 cm, its area is 1/2 x 8 cm x 6 cm = 24 cm².
3.4 Area of a Circle: Pi Times Radius Squared
The area of a circle is found by multiplying π (pi, approximately 3.14159) by the square of its radius. A circle with a radius of 3 cm has an area of π x 3 cm x 3 cm ≈ 28.27 cm².
4. Understanding Units of Measurement for “What is the Area?”
Area is measured in square units. Common units include square centimeters (cm²), square meters (m²), square inches (in²), and square feet (ft²). The choice of unit depends on the size of the area being measured.
4.1 Common Units: Square Centimeters and Meters
For smaller areas, square centimeters are often used. For larger areas like rooms or buildings, square meters are more appropriate.
4.2 Square Inches and Feet: US Standard Units
In the United States, square inches and square feet are commonly used. Square inches are suitable for small objects, while square feet are used for rooms and houses.
4.3 Converting Between Units: A Practical Guide
Converting between units is essential for accurate calculations. For example, 1 square meter is equal to 10,000 square centimeters. Understanding these conversions is crucial for practical applications.
5. Real-World Examples: Seeing “What is the Area?” in Action
Area calculations are not just theoretical exercises; they have real-world applications. Let’s explore some examples:
5.1 Calculating the Area of a Room
To determine how much flooring you need for a room, you must calculate its area. Multiply the length and width of the room to find the area in square feet or meters.
5.2 Determining the Size of a Garden
Gardeners use area calculations to determine how much space they have for planting. This helps in planning the layout and ensuring efficient use of space.
5.3 Estimating Paint for a Wall
When painting a wall, you need to know its area to estimate how much paint is required. Multiply the height and width of the wall to find the area in square feet or meters.
Here are a few ways in which you can apply the knowledge of the area of figures in your daily life.
- We can find the area of a gifting paper to check whether it will be able to cover a box or not.
- We can find the area of a square or circle to find the area of the signal board.
- The concept of area has been the foundation of geometry since the early days. Scientists and astronomers took the help of patterns and geometric shapes to understand and establish advanced concepts in science and mathematics.
- In a modern aspect, the mathematical modeling of objects such as machines, tools, wheels as well as garment designing uses the concept of area and perimeter. It also serves as a basis for integral calculus to understand complex objects such as spheres and ellipses.
6. Advanced Concepts: What is the Area of Complex Shapes?
Calculating the area of complex shapes can be more challenging, but it’s achievable by breaking down the shape into simpler components.
6.1 Composite Figures: Combining Simple Shapes
Composite figures are made up of two or more simple shapes. To find the area of a composite figure, calculate the area of each individual shape and then add them together.
These shapes formed by the combination of two or more simple shapes are called “composite figures” or “composite shapes“.
For finding the area of a composite figure, we must find the sum of the area of all the shapes in it. So, the area of the shape we just drew will be the area of the rectangle,l bplushalfthe area of the circle, ½ x πr², where l and b are the length and breadth of the rectangle and r is the radius of the semicircle.
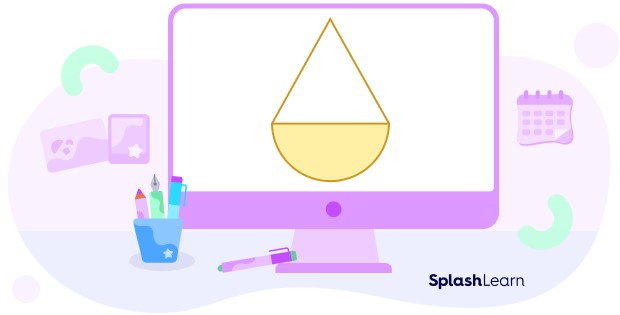
If we draw a semicircle below a triangle, we get the composite shape:
The area of such a composite figure will be calculated by adding the area of the triangle and the area of the semicircle.
Area of the a composite figure $= (frac{1}{2} times b times h) times (frac{1}{2} + pi r^{2})$
where r is the radius of the semicircle and b and h are the base and height of the triangle respectively.
6.2 Irregular Shapes: Approximations and Estimations
For irregular shapes, you can use approximations or estimations. One method is to overlay a grid and count the squares that fall within the shape.
6.3 Using Calculus: Finding Area Under a Curve
Calculus provides methods for finding the area under a curve. This is useful in various scientific and engineering applications.
7. Practice Problems: Test Your Knowledge of “What is the Area?”
Test your understanding with these practice problems:
- What is the area of a rectangle with a length of 12 cm and a width of 7 cm?
- Calculate the area of a triangle with a base of 15 cm and a height of 10 cm.
- Find the area of a circle with a radius of 6 cm.
- What is the area of a square with a side of 9 cm?
- The area of a rectangular pool is 500 sq. ft. If the width of the pool is 20 ft, what is its length?
Answers:
- 84 cm²
- 75 cm²
- 113.10 cm² (approximately)
- 81 cm²
- 25 ft
Area
Attend this Quiz & Test your knowledge.
1
The side of a square is 7 cm. What is the area of this square?
20 cm$^{2}$
30 cm$^{2}$
40 cm$^{2}$
49 cm$^{2}$
CorrectIncorrect
Correct answer is: 49 cm$^{2}$Area of the square = side $times$ side $A = 7 times 7 = 49$ $cm^{2}$
2
The height of a triangle is 25 cm and the base is 50 cm. What is the area of the triangle?
600 cm$^{2}$
625 cm$^{2}$
650 cm$^{2}$
700 cm$^{2}$
CorrectIncorrect
Correct answer is: 625 cm$^{2}$Area of the triangle $= frac{1}{2} times b times h = frac{1}{2} times 50 times 25 = 625$ $cm^{2}$
3
What is the area of a circle that has a radius of 4 cm?
$40$ $cm^{2}$
$16$ $cm^{2}$
$60.27$ $cm^{2}$
$50.27$ $cm^{2}$
CorrectIncorrect
Correct answer is: $50.27$ $cm^{2}$Area of the circle $= pi r^{2} =3.14 times 4 times 4 = 50.27$ $cm^{2}$
4
The base of a parallelogram is 50 cm and the perpendicular height is 20 cm. What is the area of this parallelogram?
$400$ $cm^{2}$
$500$ $cm^{2}$
$750$ $cm^{2}$
$1000$ $cm^{2}$
CorrectIncorrect
Correct answer is: $1000$ $cm^{2}$Area of the parallelogram $= b times h = 50 times 20 = 1000$ $cm^{2}$.
5
What is the area of a square whose perimeter is 28 m?
$21$ $m^{2}$
$42$ $m^{2}$
$49$ $m^{2}$
$47$ $m^{2}$
CorrectIncorrect
Correct answer is: $49$ $m^{2}$Perimeter of square $= 28$ m Let side of square be ‘s’ m $4 times s = 28$ $Rightarrow s = 7$ So, side of square $= 7$ m Area of square $= s times s = 7 times 7 = 49$ $m^{2}$
6
What is the area of a circle whose radius is 10 cm?
$100pi$ $m^{2}$
$300pi$ $m^{2}$
$400pi$ $m^{2}$
$500pi$ $m^{2}$
CorrectIncorrect
Correct answer is: $100pi$ $m^{2}$Area of circle $= pi r^{2} = pi times 10 times 10 = 100pi$ $m^{2}$
7
The area of a rectangular pool is 500 sq. ft. If the width of the pool is 20 ft, what is its length?
25 ft
30 ft
50 ft
100 ft
CorrectIncorrect
Correct answer is: 25 ftArea of rectangle $= text{Length} times text{Breadth}$ Length $= frac{Area}{Length} = frac{500}{20} = 25$ ft
8
What is the area of a rectangular park whose length and breadth are 80 m and 100 m respectively?
$1800$ $m^{2}$
$180$ $m^{2}$
$1018$ $m^{2}$
$8000$ $m^{2}$
CorrectIncorrect
Correct answer is: $8000$ $m^{2}$Area of rectangle $= text{Length} times text{breadth} = 80 times 100 = 8000$ $m^{2}$
8. Common Mistakes to Avoid When Calculating “What is the Area?”
Avoid these common mistakes for accurate area calculations:
8.1 Using the Wrong Formula
Make sure to use the correct formula for the shape you are calculating. Using the wrong formula will lead to incorrect results.
8.2 Mixing Units of Measurement
Ensure all measurements are in the same unit before calculating the area. Mixing units will result in inaccurate calculations.
8.3 Forgetting to Square the Units
Area is measured in square units, so remember to square the units in your final answer.
9. Frequently Asked Questions About “What is the Area?”
Let’s address some common questions about area:
9.1 How is Area Used in Real Estate?
In real estate, area is used to determine the size of a property and calculate its value.
9.2 Can Area Be Negative?
Area cannot be negative because it measures a physical space, which cannot be less than zero.
9.3 What is Surface Area?
Surface area is the total area of the surface of a three-dimensional object.
9.4 How Does Area Relate to Calculus?
Calculus provides advanced methods for finding the area under curves and complex shapes, using integration techniques.
9.5 Is Understanding Area Important for Cooking?
Yes, understanding area can be helpful in cooking, especially when scaling recipes or determining the size of baking pans.
10. Conclusion: Mastering the Concept of “What is the Area?”
Understanding area is crucial for various applications, from everyday tasks to advanced scientific calculations. By mastering the basic concepts, formulas, and units of measurement, you can confidently tackle area-related problems.
10.1 Recap of Key Concepts
- Area is the measure of the surface of a two-dimensional shape.
- The formula for calculating area varies depending on the shape.
- Area is measured in square units.
- Real-world applications include home improvement, gardening, and construction.
10.2 Final Thoughts on the Importance of Understanding Area
A solid grasp of area is essential for problem-solving, analytical thinking, and success in various fields. Keep practicing and exploring real-world applications to deepen your understanding.
Still have questions about area or other topics? Don’t hesitate to ask on WHAT.EDU.VN, where you can get free answers to all your questions. Our community of experts is ready to help you understand complex concepts and solve problems.
Address: 888 Question City Plaza, Seattle, WA 98101, United States
WhatsApp: +1 (206) 555-7890
Website: WHAT.EDU.VN
At what.edu.vn, we believe that everyone should have access to free, reliable information. Ask your questions today and let us help you on your learning journey.