What Is The Formula For Area? If you’re asking this question, you’re in the right place! At WHAT.EDU.VN, we understand the importance of grasping fundamental mathematical concepts. This guide provides a comprehensive overview of area formulas for various shapes and geometrical figures, ensuring that students, professionals, and curious minds alike can easily understand and apply these formulas. If you have further questions, remember that WHAT.EDU.VN is here to provide free answers and assistance.
Table of Contents
-
Understanding Area: The Basics
-
Area Formulas for Basic Shapes
- 2.1. Area of a Square
- 2.2. Area of a Rectangle
- 2.3. Area of a Triangle
- 2.4. Area of a Circle
- 2.5. Area of a Parallelogram
- 2.6. Area of a Trapezoid
- 2.7. Area of an Ellipse
-
Area Formulas for Complex Shapes
- 3.1. Area of a Rhombus
- 3.2. Area of a Kite
- 3.3. Area of a Hexagon
- 3.4. Area of a Pentagon
-
Area and Perimeter: Understanding the Difference
-
Practical Applications of Area Formulas
- 5.1. Real-World Examples
- 5.2. Common Mistakes to Avoid
-
Advanced Concepts Related to Area
- 6.1. Area of Irregular Shapes
- 6.2. Area in Coordinate Geometry
- 6.3. Area in Calculus
-
Historical Perspective on Area Calculation
-
Tips and Tricks for Memorizing Area Formulas
-
Frequently Asked Questions (FAQs) about Area
-
Conclusion: Mastering Area with WHAT.EDU.VN
1. Understanding Area: The Basics
Area, in simple terms, is the amount of two-dimensional space a shape occupies. It’s a fundamental concept in geometry and is used in various fields, from architecture and engineering to everyday tasks like calculating the size of a room or a garden. Understanding area involves knowing the formulas to calculate the space enclosed within different shapes. The concept is crucial not only for academic success but also for practical applications in real life.
Area is measured in square units, such as square meters (m²), square feet (ft²), square inches (in²), or square centimeters (cm²). These units indicate that we are measuring the space in two dimensions. The formula you use to calculate area depends entirely on the shape you’re working with.
2. Area Formulas for Basic Shapes
2.1. Area of a Square
A square is a quadrilateral with four equal sides and four right angles. The formula for the area of a square is straightforward:
Formula: Area = a²
where a is the length of one side of the square.
Example: If a square has a side length of 5 cm, then its area is 5² = 25 cm².
This formula is essential for various applications, from calculating the area of tiles to designing square-shaped structures.
2.2. Area of a Rectangle
A rectangle is a quadrilateral with two pairs of equal sides and four right angles. The formula for the area of a rectangle is:
Formula: Area = l × w
where l is the length and w is the width of the rectangle.
Example: If a rectangle has a length of 8 meters and a width of 4 meters, then its area is 8 × 4 = 32 m².
Rectangles are common in many real-world scenarios, such as rooms, fields, and screens, making this formula highly practical.
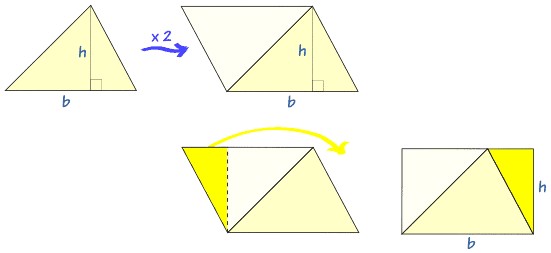
2.3. Area of a Triangle
A triangle is a three-sided polygon. The most common formula for the area of a triangle is:
Formula: Area = 1/2 × b × h
where b is the base and h is the height of the triangle. The height is the perpendicular distance from the base to the opposite vertex.
There are other formulas to calculate the area of a triangle, such as Heron’s formula, which is used when you know the lengths of all three sides:
Heron’s Formula: Area = √[s(s-a)(s-b)(s-c)]
where a, b, and c are the lengths of the sides, and s is the semi-perimeter of the triangle, calculated as:
s = (a + b + c) / 2
Example: For a triangle with a base of 10 cm and a height of 7 cm, the area is 1/2 × 10 × 7 = 35 cm².
Triangles appear in various contexts, from structural engineering to artistic designs, making the area calculation crucial.
2.4. Area of a Circle
A circle is a set of points equidistant from a central point. The formula for the area of a circle is:
Formula: Area = πr²
where r is the radius of the circle, and π (pi) is approximately 3.14159.
Example: If a circle has a radius of 6 inches, then its area is π × 6² ≈ 113.097 inches².
Circles are fundamental in many applications, including mechanical engineering and design.
2.5. Area of a Parallelogram
A parallelogram is a quadrilateral with two pairs of parallel sides. The formula for the area of a parallelogram is:
Formula: Area = b × h
where b is the base and h is the height of the parallelogram. The height is the perpendicular distance between the base and the opposite side.
Example: If a parallelogram has a base of 12 cm and a height of 5 cm, then its area is 12 × 5 = 60 cm².
Parallelograms are important in understanding vector addition and are found in various engineering applications.
2.6. Area of a Trapezoid
A trapezoid (or trapezium) is a quadrilateral with at least one pair of parallel sides. The formula for the area of a trapezoid is:
Formula: Area = 1/2 × (a + b) × h
where a and b are the lengths of the parallel sides, and h is the height (the perpendicular distance between the parallel sides).
Example: If a trapezoid has parallel sides of lengths 7 cm and 11 cm, and a height of 4 cm, then its area is 1/2 × (7 + 11) × 4 = 36 cm².
Trapezoids are encountered in architecture and structural design.
2.7. Area of an Ellipse
An ellipse is a stretched circle. The formula for the area of an ellipse is:
Formula: Area = πab
where a is the length of the semi-major axis and b is the length of the semi-minor axis.
Example: If an ellipse has a semi-major axis of 9 cm and a semi-minor axis of 5 cm, then its area is π × 9 × 5 ≈ 141.372 cm².
Ellipses are used in astronomy (planetary orbits) and optics.
3. Area Formulas for Complex Shapes
3.1. Area of a Rhombus
A rhombus is a quadrilateral with four equal sides and opposite angles being equal. The formula for the area of a rhombus can be calculated in two ways:
Formula 1: Area = 1/2 × d1 × d2
where d1 and d2 are the lengths of the diagonals.
Formula 2: Area = b × h
where b is the base and h is the height.
Example: If a rhombus has diagonals of lengths 10 cm and 8 cm, then its area is 1/2 × 10 × 8 = 40 cm².
Rhombuses are found in tessellations and various geometric designs.
3.2. Area of a Kite
A kite is a quadrilateral with two pairs of adjacent sides that are equal in length. The formula for the area of a kite is:
Formula: Area = 1/2 × d1 × d2
where d1 and d2 are the lengths of the diagonals.
Example: If a kite has diagonals of lengths 14 cm and 6 cm, then its area is 1/2 × 14 × 6 = 42 cm².
Kites are commonly used in recreational activities and are studied in geometry.
3.3. Area of a Hexagon
A hexagon is a six-sided polygon. A regular hexagon, where all sides and angles are equal, has a specific area formula:
Formula: Area = (3√3 / 2) × a²
where a is the length of one side of the hexagon.
Example: If a regular hexagon has a side length of 4 cm, then its area is (3√3 / 2) × 4² ≈ 41.569 cm².
Hexagons are found in nature (honeycombs) and engineering (nuts and bolts).
3.4. Area of a Pentagon
A pentagon is a five-sided polygon. For a regular pentagon, where all sides and angles are equal, the area formula is:
Formula: Area = (1/4) × √[5(5 + 2√5)] × a²
where a is the length of one side of the pentagon.
Example: If a regular pentagon has a side length of 5 cm, then its area is (1/4) × √[5(5 + 2√5)] × 5² ≈ 43.012 cm².
Pentagons are less common but appear in architectural designs and geometric patterns.
4. Area and Perimeter: Understanding the Difference
It’s crucial to differentiate between area and perimeter. Area measures the space enclosed within a shape, while perimeter measures the length of the boundary of the shape.
For example, consider a square with a side length of 4 cm:
- Area = a² = 4² = 16 cm²
- Perimeter = 4a = 4 × 4 = 16 cm
In this case, the numerical values of area and perimeter are the same, but they represent different concepts and have different units (cm² for area and cm for perimeter).
Understanding this difference is essential to avoid confusion and apply the correct formulas in problem-solving.
5. Practical Applications of Area Formulas
5.1. Real-World Examples
Area formulas are used extensively in various real-world scenarios:
- Construction: Calculating the amount of material needed for flooring, roofing, or painting.
- Agriculture: Determining the size of a field for planting crops.
- Interior Design: Planning the layout of furniture in a room.
- Engineering: Designing structures and calculating stress distribution.
- Real Estate: Assessing the value of a property based on its size.
5.2. Common Mistakes to Avoid
When working with area formulas, avoid these common mistakes:
- Using the wrong units: Ensure all measurements are in the same unit before calculating the area.
- Confusing area and perimeter: Remember that area measures space inside a shape, while perimeter measures the length of the boundary.
- Incorrectly identifying shape dimensions: Make sure to use the correct base, height, and side lengths in the formulas.
- Forgetting the units in the final answer: Always include the appropriate square units (e.g., cm², m², ft²) in your answer.
6. Advanced Concepts Related to Area
6.1. Area of Irregular Shapes
Calculating the area of irregular shapes can be challenging. One common method is to divide the irregular shape into smaller, regular shapes (e.g., triangles, rectangles) and sum their areas.
Another approach is to use numerical methods, such as the trapezoidal rule or Simpson’s rule, to approximate the area. These methods are commonly used in calculus and computational geometry.
6.2. Area in Coordinate Geometry
In coordinate geometry, the area of a polygon can be calculated using the coordinates of its vertices. The formula for the area of a triangle with vertices (x1, y1), (x2, y2), and (x3, y3) is:
Area = 1/2 |x1(y2 – y3) + x2(y3 – y1) + x3(y1 – y2)|
For more complex polygons, the Shoelace Theorem can be used to calculate the area.
6.3. Area in Calculus
Calculus provides powerful tools for calculating areas under curves. The area under a curve y = f(x) between x = a and x = b is given by the definite integral:
Area = ∫ab f(x) dx
This concept is fundamental in physics, engineering, and economics, where areas under curves represent quantities like work, distance, and consumer surplus.
7. Historical Perspective on Area Calculation
The concept of area has been around for thousands of years, dating back to ancient civilizations like the Egyptians and Babylonians. They needed to calculate areas for land surveying, construction, and taxation purposes.
The Greeks, particularly Euclid and Archimedes, made significant contributions to the understanding of area. Euclid’s “Elements” provided a rigorous foundation for geometry, while Archimedes developed methods for calculating the areas of circles and other curved shapes.
In the 17th century, the development of calculus by Isaac Newton and Gottfried Wilhelm Leibniz revolutionized area calculation, providing powerful tools for handling complex shapes and curves.
8. Tips and Tricks for Memorizing Area Formulas
Memorizing area formulas can be made easier with these tips and tricks:
- Use flashcards: Write the name of the shape on one side and the area formula on the other.
- Create mnemonic devices: Develop memorable phrases or acronyms to help you remember the formulas.
- Practice regularly: Solve a variety of problems involving different shapes and area formulas.
- Understand the formulas: Instead of just memorizing, try to understand why each formula works.
- Draw diagrams: Visual aids can help you remember the formulas and their applications.
9. Frequently Asked Questions (FAQs) about Area
Q1: What is the formula for the area of a square?
A: The formula for the area of a square is Area = a², where a is the length of one side of the square.
Q2: How do you calculate the area of a rectangle?
A: The area of a rectangle is calculated using the formula Area = l × w, where l is the length and w is the width of the rectangle.
Q3: What is the formula for the area of a circle?
A: The formula for the area of a circle is Area = πr², where r is the radius of the circle and π (pi) is approximately 3.14159.
Q4: How do you find the area of a triangle?
A: The area of a triangle can be found using the formula Area = 1/2 × b × h, where b is the base and h is the height of the triangle. Alternatively, you can use Heron’s formula if you know the lengths of all three sides.
Q5: What is the difference between area and perimeter?
A: Area measures the space enclosed within a shape, while perimeter measures the length of the boundary of the shape.
Q6: How do you calculate the area of an irregular shape?
A: Divide the irregular shape into smaller, regular shapes (e.g., triangles, rectangles) and sum their areas. Alternatively, use numerical methods like the trapezoidal rule.
Q7: Can you use the area formula in real life?
A: Yes, area formulas are used extensively in various real-world scenarios, such as construction, agriculture, interior design, engineering, and real estate.
Q8: What should I do if I’m struggling to memorize the formulas?
A: Use flashcards, create mnemonic devices, practice regularly, understand the formulas, and draw diagrams to help you remember the formulas and their applications.
Q9: What is the area of a parallelogram if the base is 10cm and the height is 5cm?
A: The area of the parallelogram is Area = b × h = 10 cm × 5 cm = 50 cm².
Q10: What is the area of a trapezoid with parallel sides of lengths 6cm and 8cm and a height of 4cm?
A: The area of the trapezoid is Area = 1/2 × (a + b) × h = 1/2 × (6 cm + 8 cm) × 4 cm = 28 cm².
For more questions and detailed explanations, visit WHAT.EDU.VN.
10. Conclusion: Mastering Area with WHAT.EDU.VN
Understanding area formulas is crucial for success in mathematics and various real-world applications. This comprehensive guide has covered the essential area formulas for basic and complex shapes, practical applications, advanced concepts, and tips for memorization.
At WHAT.EDU.VN, we are dedicated to providing free, accurate, and easy-to-understand answers to all your questions. Whether you’re a student, a professional, or simply a curious mind, our platform is here to support your learning journey.
Do you have more questions about area or any other topic? Don’t hesitate to ask! Visit WHAT.EDU.VN today and get the answers you need. Our team of experts is ready to assist you with any questions you might have.
Contact Us:
- Address: 888 Question City Plaza, Seattle, WA 98101, United States
- WhatsApp: +1 (206) 555-7890
- Website: WHAT.EDU.VN
Take the next step in your learning journey with what.edu.vn!