What Is The Hardest Math Problem? The perception of difficulty in mathematics is subjective and varies greatly from person to person. At WHAT.EDU.VN, we delve into the complexities of mathematical challenges, offering insights and solutions to help learners of all levels overcome their obstacles, providing free support and answers to even the most difficult inquiries. With a little effort, you can conquer even the most seemingly impossible math questions.
1. Understanding the Elusive “Hardest” Math Problem
What constitutes the most difficult math problem? It’s a question that has plagued mathematicians and students alike for centuries. The truth is, there is no single “hardest” problem, as difficulty is subjective and depends on an individual’s background, knowledge, and problem-solving skills. However, certain problems are widely recognized for their complexity and the significant effort required to solve them.
2. Factors Contributing to Difficulty in Math
Several factors contribute to the perceived difficulty of a math problem:
- Abstract Concepts: Problems dealing with abstract concepts like higher-dimensional spaces, complex numbers, or advanced set theory can be challenging because they require a strong understanding of theoretical frameworks.
- Multiple Steps: Problems involving numerous steps or requiring the integration of several mathematical concepts can be difficult to manage and solve accurately.
- Lack of Familiarity: Unfamiliarity with a particular mathematical topic or technique can make a problem seem more difficult than it actually is.
- Convoluted Wording: Problems with complex or ambiguous wording can be challenging to understand and interpret, leading to confusion and difficulty in finding a solution.
- Extensive Variable Use: Problems that incorporate a large number of variables can be confusing and require careful tracking and manipulation to solve.
3. Famous Unsolved Math Problems
Throughout history, numerous math problems have remained unsolved for decades or even centuries, capturing the imagination of mathematicians and inspiring countless hours of research. Some of the most famous unsolved problems include:
- The Riemann Hypothesis: This hypothesis, formulated by Bernhard Riemann in 1859, concerns the distribution of prime numbers and has profound implications for number theory.
- Goldbach’s Conjecture: This conjecture, proposed by Christian Goldbach in 1742, states that every even integer greater than 2 can be expressed as the sum of two prime numbers.
- The Twin Prime Conjecture: This conjecture posits that there are infinitely many pairs of prime numbers that differ by 2 (e.g., 3 and 5, 5 and 7, 11 and 13).
- The Collatz Conjecture: Also known as the 3n+1 problem, this conjecture involves a simple iterative sequence that, starting from any positive integer, is conjectured to always reach 1.
4. The Hardest SAT Math Questions: A Glimpse
The SAT Math section is designed to assess a student’s mathematical reasoning and problem-solving skills. While the test primarily focuses on concepts learned in high school, some questions can be particularly challenging. These problems often:
- Integrate multiple mathematical concepts
- Require numerous steps to solve
- Involve less familiar topics
- Are worded in unusual or complex ways
- Use many different variables
Let’s examine some examples of these challenging SAT Math questions, with explanations to help understand their difficulty and how to approach them.
4.1. Sample Question 1
Question:
C = 5/9(F - 32)The equation above shows how temperature $F$, measured in degrees Fahrenheit, relates to a temperature $C$, measured in degrees Celsius. Based on the equation, which of the following must be true?
I. A temperature increase of 1 degree Fahrenheit is equivalent to a temperature increase of $5/9$ degree Celsius.
II. A temperature increase of 1 degree Celsius is equivalent to a temperature increase of 1.8 degrees Fahrenheit.
III. A temperature increase of $5/9$ degree Fahrenheit is equivalent to a temperature increase of 1 degree Celsius.
A) I only
B) II only
C) III only
D) I and II only
Answer Explanation:
Think of the equation as an equation for a line:
$$y = mx + b$$
where in this case:
$$C= {5}/{9} (F−32)$$
or
$$C={5}/{9}F −{5}/{9}(32)$$
You can see the slope of the graph is ${5}/{9}$, which means that for an increase of 1 degree Fahrenheit, the increase is ${5}/{9}$ of 1 degree Celsius.
$$C= {5}/{9} (F)$$
$$C= {5}/{9} (1)= {5}/{9}$$
Therefore, statement I is true. This is the equivalent to saying that an increase of 1 degree Celsius is equal to an increase of ${9}/{5}$ degrees Fahrenheit.
$$C= {5}/{9} (F)$$
$$1= {5}/{9} (F)$$
$$(F)={9}/{5}$$
Since ${9}/{5}$ = 1.8, statement II is true.
The only answer that has both statement I and statement II as true is D, but if you have time and want to be absolutely thorough, you can also check to see if statement III (an increase of ${5}/{9}$ degree Fahrenheit is equal to a temperature increase of 1 degree Celsius) is true:
$$C= {5}/{9} (F)$$
$$C= {5}/{9} ({5}/{9})$$
$$C= {25} /{81} (which is ≠ 1)$$
An increase of $5/9$ degree Fahrenheit leads to an increase of ${25}/{81}$, not 1 degree, Celsius, and so Statement III is not true.
The final answer is D.
4.2. Sample Question 2
Question:
The equation $frac{24x^2 + 25x -47}{ax-2} = -8x-3-frac{53}{ax-2}$ is true for all values of $x neq frac{2}{a}$, where $a$ is a constant.
What is the value of $a$?
A) -16
B) -3
C) 3
D) 16
Answer Explanation:
There are two ways to solve this question. The faster way is to multiply each side of the given equation by $ax-2$ (so you can get rid of the fraction). When you multiply each side by $ax-2$, you should have:
$$24x^2 + 25x – 47 = (-8x-3)(ax-2) – 53$$
You should then multiply $(-8x-3)$ and $(ax-2)$ using FOIL.
$$24x^2 + 25x – 47 = -8ax^2 – 3ax +16x + 6 – 53$$
Then, reduce on the right side of the equation
$$24x^2 + 25x – 47 = -8ax^2 – 3ax +16x – 47$$
Since the coefficients of the $x^2$-term have to be equal on both sides of the equation, $−8a = 24$, or $a = −3$.
The other option which is longer and more tedious is to attempt to plug in all of the answer choices for a and see which answer choice makes both sides of the equation equal. Again, this is the longer option, and I do not recommend it for the actual SAT as it will waste too much time.
The final answer is B.
4.3. Sample Question 3
Question:
If $3x-y = 12$, what is the value of $frac{8^x}{2^y}$?
A) $2^{12}$
B) $4^4$
C) $8^2$
D) The value cannot be determined from the information given.
Answer Explanation:
One approach is to express
$$frac{8^x}{2^y}$$
so that the numerator and denominator are expressed with the same base. Since 2 and 8 are both powers of 2, substituting $2^3$ for 8 in the numerator of $frac{8^x}{2^y}$ gives
$$frac{(2^3)^x}{2^y}$$
which can be rewritten
$$frac{2^{3x}}{2^y}$$
Since the numerator and denominator of have a common base, this expression can be rewritten as $2^{3x-y}$. In the question, it states that $3x − y = 12$, so one can substitute 12 for the exponent, $3x − y$, which means that
$$frac{8^x}{2^y}= 2^{12}$$
The final answer is A.
4.4. Sample Question 4
Question:
Points A and B lie on a circle with radius 1, and arc $stackrel{frown}{AB}$ has a length of $frac{pi}{3}$. What fraction of the circumference of the circle is the length of arc $stackrel{frown}{AB}$?
Answer Explanation:
To figure out the answer to this question, you’ll first need to know the formula for finding the circumference of a circle.
The circumference, $C$, of a circle is $C = 2pi r$, where $r$ is the radius of the circle. For the given circle with a radius of 1, the circumference is $C = 2(pi)(1)$, or $C = 2pi$.
To find what fraction of the circumference the length of $stackrel{frown}{AB}$ is, divide the length of the arc by the circumference, which gives $frac{pi}{3} div 2pi$. This division can be represented by $frac{pi}{3} * frac{1}{2pi} = frac{1}{6}$.
The fraction $frac{1}{6}$ can also be rewritten as $0.166$ or $0.167$.
The final answer is $frac{1}{6}$, $0.166$, or $0.167$.
4.5. Sample Question 5
Question:
$$frac{8-i}{3-2i}$$
If the expression above is rewritten in the form $a+bi$, where $a$ and $b$ are real numbers, what is the value of $a$? (Note: $i=sqrt{-1}$)
Answer Explanation:
To rewrite $frac{8-i}{3-2i}$ in the standard form $a + bi$, you need to multiply the numerator and denominator of $frac{8-i}{3-2i}$ by the conjugate, $3 + 2i$. This equals
$$(frac{8-i}{3-2i})(frac{3+2i}{3+2i})=frac{24+16i-3i+(-i)(2i)}{(3^2)-(2i)^2}$$
Since $i^2=-1$, this last fraction can be reduced simplified to
$$ frac{24+16i-3i+2}{9-(-4)}=frac{26+13i}{13}$$
which simplifies further to $2 + i$. Therefore, when $frac{8-i}{3-2i}$ is rewritten in the standard form a + bi, the value of a is 2.
The final answer is A.
4.6. Sample Question 6
Question:
In triangle $ABC$, the measure of $angle B$ is 90°, $BC=16$, and $AC=20$. Triangle $DEF$ is similar to triangle $ABC$, where vertices $D$, $E$, and $F$ correspond to vertices $A$, $B$, and $C$, respectively, and each side of triangle $DEF$ is $frac{1}{3}$ the length of the corresponding side of triangle $ABC$. What is the value of $sinF$?
Answer Explanation:
Triangle ABC is a right triangle with its right angle at B. Therefore, $overline{AC}$ is the hypotenuse of right triangle ABC, and $overline{AB}$ and $overline{BC}$ are the legs of right triangle ABC. According to the Pythagorean theorem,
$$AB =sqrt{20^2-16^2}=sqrt{400-256}=sqrt{144}=12$$
Since triangle DEF is similar to triangle ABC, with vertex F corresponding to vertex C, the measure of $angle F$ equals the measure of $angle C$. Therefore, $sin F = sin C$. From the side lengths of triangle ABC,
$$sinF =frac{text{opposite side}}{text{hypotenuse}}=frac{AB}{AC}=frac{12}{20}=frac{3}{5}$$
Therefore, $sinF =frac{3}{5}$.
The final answer is $frac{3}{5}$ or 0.6.
4.7. Sample Question 7
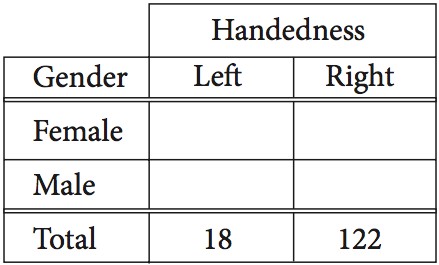
Question:
The incomplete table above summarizes the number of left-handed students and right-handed students by gender for the eighth grade students at Keisel Middle School. There are 5 times as many right-handed female students as there are left-handed female students, and there are 9 times as many right-handed male students as there are left-handed male students. if there is a total of 18 left-handed students and 122 right-handed students in the school, which of the following is closest to the probability that a right-handed student selected at random is female? (Note: Assume that none of the eighth-grade students are both right-handed and left-handed.)
A) 0.410
B) 0.357
C) 0.333
D) 0.250
Answer Explanation:
In order to solve this problem, you should create two equations using two variables ($x$ and $y$) and the information you’re given. Let $x$ be the number of left-handed female students and let $y$ be the number of left-handed male students. Using the information given in the problem, the number of right-handed female students will be $5x$ and the number of right-handed male students will be $9y$. Since the total number of left-handed students is 18 and the total number of right-handed students is 122, the system of equations below must be true:
$$x + y = 18$$
$$5x + 9y = 122$$
When you solve this system of equations, you get $x = 10$ and $y = 8$. Thus, 5*10, or 50, of the 122 right-handed students are female. Therefore, the probability that a right-handed student selected at random is female is $frac{50}{122}$, which to the nearest thousandth is 0.410.
The final answer is A.
4.8. Sample Question 8 & 9
Question:
Use the following information for both question 7 and question 8.
If shoppers enter a store at an average rate of $r$ shoppers per minute and each stays in the store for average time of $T$ minutes, the average number of shoppers in the store, $N$, at any one time is given by the formula $N=rT$. This relationship is known as Little’s law.
The owner of the Good Deals Store estimates that during business hours, an average of 3 shoppers per minute enter the store and that each of them stays an average of 15 minutes. The store owner uses Little’s law to estimate that there are 45 shoppers in the store at any time.
Question 8:
Little’s law can be applied to any part of the store, such as a particular department or the checkout lines. The store owner determines that, during business hours, approximately 84 shoppers per hour make a purchase and each of these shoppers spend an average of 5 minutes in the checkout line. At any time during business hours, about how many shoppers, on average, are waiting in the checkout line to make a purchase at the Good Deals Store?
Answer Explanation:
Since the question states that Little’s law can be applied to any single part of the store (for example, just the checkout line), then the average number of shoppers, $N$, in the checkout line at any time is $N = rT$, where $r$ is the number of shoppers entering the checkout line per minute and $T$ is the average number of minutes each shopper spends in the checkout line.
Since 84 shoppers per hour make a purchase, 84 shoppers per hour enter the checkout line. However, this needs to be converted to the number of shoppers per minute (in order to be used with $T = 5$). Since there are 60 minutes in one hour, the rate is $frac{84 text{ shoppers per hour}}{60 text{ minutes}} = 1.4$ shoppers per minute. Using the given formula with $r = 1.4$ and $T = 5$ yields
$$N = rt = (1.4)(5) = 7$$
Therefore, the average number of shoppers, $N$, in the checkout line at any time during business hours is 7.
The final answer is 7.
Question 9:
The owner of the Good Deals Store opens a new store across town. For the new store, the owner estimates that, during business hours, an average of 90 shoppers per hour enter the store and each of them stays an average of 12 minutes. The average number of shoppers in the new store at any time is what percent less than the average number of shoppers in the original store at any time? (Note: Ignore the percent symbol when entering your answer. For example, if the answer is 42.1%, enter 42.1)
Answer Explanation:
According to the original information given, the estimated average number of shoppers in the original store at any time (N) is 45. In the question, it states that, in the new store, the manager estimates that an average of 90 shoppers per hour (60 minutes) enter the store, which is equivalent to 1.5 shoppers per minute (r). The manager also estimates that each shopper stays in the store for an average of 12 minutes (T). Thus, by Little’s law, there are, on average, $N = rT = (1.5)(12) = 18$ shoppers in the new store at any time. This is
$$frac{45-18}{45} * 100 = 60$$
percent less than the average number of shoppers in the original store at any time.
The final answer is 60.
4.9. Sample Question 10
Question:
In the $xy$-plane, the point $(p,r)$ lies on the line with equation $y=x+b$, where $b$ is a constant. The point with coordinates $(2p, 5r)$ lies on the line with equation $y=2x+b$. If $pneq 0$, what is the value of $frac{r}{p}$?
A) $frac{2}{5}$
B) $frac{3}{4}$
C) $frac{4}{3}$
D) $frac{5}{2}$
Answer Explanation:
Since the point $(p,r)$ lies on the line with equation $y=x+b$, the point must satisfy the equation. Substituting $p$ for $x$ and $r$ for $y$ in the equation $y=x+b$ gives $r=p+b$, or $b = r-p$.
Similarly, since the point $(2p,5r)$ lies on the line with the equation $y=2x+b$, the point must satisfy the equation. Substituting $2p$ for $x$ and $5r$ for $y$ in the equation $y=2x+b$ gives:
$$5r=2(2p)+b$$
$$5r=4p+b$$
$$b = 5r-4p$$.
Next, we can set the two equations equal to $b$ equal to each other and simplify:
$$b=r-p=5r-4p$$
$$3p=4r$$
Finally, to find $frac{r}{p}$, we need to divide both sides of the equation by $p$ and by $4$:
$$3p=4r$$
$$3=frac{4r}{p}$$
$$frac{3}{4}=frac{r}{p}$$
The correct answer is B, $frac{3}{4}$.
If you picked choices A and D, you may have incorrectly formed your answer out of the coefficients in the point $(2p, 5r)$. If you picked Choice C, you may have confused $r$ and $p$.
Note that while this is in the calculator section of the SAT, you absolutely do not need your calculator to solve it!
4.10. Sample Question 11
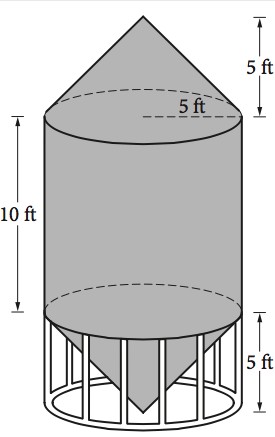
Question:
A grain silo is built from two right circular cones and a right circular cylinder with internal measurements represented by the figure above. Of the following, which is closest to the volume of the grain silo, in cubic feet?
A) 261.8
B) 785.4
C) 916.3
D) 1047.2
Answer Explanation:
The volume of the grain silo can be found by adding the volumes of all the solids of which it is composed (a cylinder and two cones). The silo is made up of a cylinder (with height 10 feet and base radius 5 feet) and two cones (each with height 5 ft and base radius 5 ft). The formulas given at the beginning of the SAT Math section:
Volume of a Cone
$$V=frac{1}{3}pi r^2h$$
Volume of a Cylinder
$$V=pi r^2h$$
can be used to determine the total volume of the silo. Since the two cones have identical dimensions, the total volume, in cubic feet, of the silo is given by
$$V_{text{silo}}=pi(5^2)(10)+(2)(frac{1}{3})pi(5^2)(5)=(frac{4}{3})(250)pi$$
which is approximately equal to 1,047.2 cubic feet.
The final answer is D.
4.11. Sample Question 12
Question:
If $x$ is the average (arithmetic mean) of $m$ and $9$, $y$ is the average of $2m$ and $15$, and $z$ is the average of $3m$ and $18$, what is the average of $x$, $y$, and $z$ in terms of $m$?
A) $m+6$
B) $m+7$
C) $2m+14$
D) $3m + 21$
Answer Explanation:
Since the average (arithmetic mean) of two numbers is equal to the sum of the two numbers divided by 2, the equations $x=frac{m+9}{2}$, $y=frac{2m+15}{2}$, $z=frac{3m+18}{2}$are true. The average of $x$, $y$, and $z$ is given by $frac{x + y + z}{3}$. Substituting the expressions in m for each variable ($x$, $y$, $z$) gives
$$[frac{m+9}{2}+frac{2m+15}{2}+frac{3m+18}{2}]/3$$
This fraction can be simplified to $m + 7$.
The final answer is B.
4.12. Sample Question 13
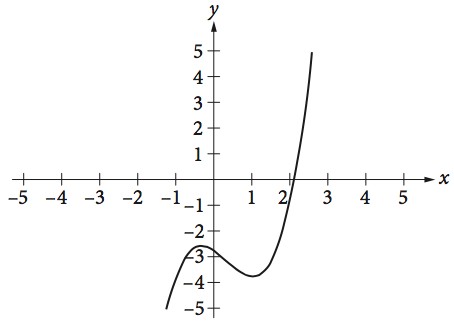
Question:
The function $f(x)=x^3-x^2-x-frac{11}{4}$ is graphed in the $xy$-plane above. If $k$ is a constant such that the equation $f(x)=k$ has three real solutions, which of the following could be the value of $k$?
A) -4
B) -1
C) 0
D) -3
Answer Explanation:
The equation $f(x) = k$ gives the solutions to the system of equations
$$y = f(x) = x^3-x^2-x-frac{11}{4}$$
and
$$y = k$$
A real solution of a system of two equations corresponds to a point of intersection of the graphs of the two equations in the $xy$-plane.
The graph of $y = k$ is a horizontal line that contains the point $(0, k)$ and intersects the graph of the cubic equation three times (since it has three real solutions). Given the graph, the only horizontal line that would intersect the cubic equation three times is the line with the equation $y = −3$, or $f(x) = −3$. Therefore, $k$ is $-3$.
The final answer is D.
4.13. Sample Question 14
Question:
$$q=frac{1}{2}nv^2$$
The dynamic pressure $q$ generated by a fluid moving with velocity $v$ can be found using the formula above, where $n$ is the constant density of the fluid. An aeronautical engineer users the formula to find the dynamic pressure of a fluid moving with velocity $v$ and the same fluid moving with velocity 1.5$v$. What is the ratio of the dynamic pressure of the faster fluid to the dynamic pressure of the slower fluid?
Answer Explanation:
To solve this problem, you need to set up to equations with variables. Let $q_1$ be the dynamic pressure of the slower fluid moving with velocity $v_1$, and let $q_2$ be the dynamic pressure of the faster fluid moving with velocity $v_2$. Then
$$v_2 =1.5v_1$$
Given the equation $q = frac{1}{2}nv^2$, substituting the dynamic pressure and velocity of the faster fluid gives $q_2 = frac{1}{2}n(v_2)^2$. Since $v_2 =1.5v_1$, the expression $1.5v_1$ can be substituted for $v_2$ in this equation, giving $q_2 = frac{1}{2}n(1.5v_1)^2$. By squaring $1.5$, you can rewrite the previous equation as
$$q_2 = (2.25)(frac{1}{2})n(v_1)^2 = (2.25)q_1$$
Therefore, the ratio of the dynamic pressure of the faster fluid is
$$frac{q2}{q1} = frac{2.25 q_1}{q_1}= 2.25$$
The final answer is 2.25 or 9/4.
4.14. Sample Question 15
Question:
For a polynomial $p(x)$, the value of $p(3)$ is $-2$. Which of the following must be true about $p(x)$?
A) $x-5$ is a factor of $p(x)$.
B) $x-2$ is a factor of $p(x)$.
C) $x+2$ is a factor of $p(x)$.
D) The remainder when $p(x)$ is divided by $x-3$ is $-2$.
Answer Explanation:
If the polynomial $p(x)$ is divided by a polynomial of the form $x+k$ (which accounts for all of the possible answer choices in this question), the result can be written as
$$frac{p(x)}{x+k}=q(x)+frac{r}{x+k}$$
where $q(x)$ is a polynomial and $r$ is the remainder. Since $x + k$ is a degree-1 polynomial (meaning it only includes $x^1$ and no higher exponents), the remainder is a real number.
Therefore, $p(x)$ can be rewritten as $p(x) = (x + k)q(x) + r$, where $r$ is a real number.
The question states that $p(3) = -2$, so it must be true that
$$-2 = p(3) = (3 + k)q(3) + r$$
Now we can plug in all the possible answers. If the answer is A, B, or C, $r$ will be $0$, while if the answer is D, $r$ will be $-2$.
A. $-2 = p(3) = (3 + (-5))q(3) + 0$
$-2=(3-5)q(3)$
$-2=(-2)q(3)$
This could be true, but only if $q(3)=1$
B. $-2 = p(3) = (3 + (-2))q(3) + 0$
$-2 = (3-2)q(3)$
$-2 = (-1)q(3)$
This could be true, but only if $q(3)=2$
C. $-2 = p(3) = (3 + 2)q(3) + 0$
$-2 = (5)q(3)$
This could be true, but only if $q(3)=frac{-2}{5}$
D. $-2 = p(3) = (3 + (-3))q(3) + (-2)$
$-2 = (3 – 3)q(3) + (-2)$
$-2 = (0)q(3) + (-2)$
This will always be true no matter what $q(3)$ is.
Of the answer choices, the only one that must be true about $p(x)$ is D, that the remainder when $p(x)$ is divided by $x-3$ is -2.
The final answer is D.
5. Mastering Difficult Math Problems: Strategies and Techniques
While there’s no magic bullet for solving difficult math problems, there are several strategies and techniques that can significantly improve your problem-solving abilities:
- Understand the Fundamentals: A strong foundation in basic mathematical concepts is essential for tackling more complex problems. Review fundamental principles and ensure you have a solid grasp of key definitions, theorems, and formulas.
- Break Down the Problem: Divide the problem into smaller, more manageable parts. Identify the core concepts involved and try to solve each part separately before combining them to find the overall solution.
- Draw Diagrams and Visual Aids: Visualizing the problem can often provide valuable insights and help you identify relationships and patterns that might not be immediately apparent.
- Work Backward: Start with the desired result and work backward, step by step, to identify the initial conditions or steps needed to reach that result.
- Look for Patterns: Many math problems involve underlying patterns or sequences. Identifying these patterns can help you simplify the problem and find a solution more efficiently.
- Use Examples: Try solving similar problems or working through examples to gain a better understanding of the concepts involved and develop your problem-solving skills.
- Don’t Give Up: Some math problems require persistence and determination. Don’t be discouraged if you don’t find a solution immediately. Keep trying different approaches and seek help when needed.
6. The Role of Experience and Practice
Like any skill, mathematical problem-solving improves with experience and practice. The more problems you solve, the more familiar you become with different types of problems and techniques, and the better you are able to approach new challenges.
Engage in regular practice, work through a variety of problems, and seek feedback from teachers, mentors, or peers to identify areas for improvement.
7. Free Math Help at WHAT.EDU.VN
At WHAT.EDU.VN, we understand the challenges students face when tackling difficult math problems. That’s why we offer a platform where you can ask any math question and receive free answers from our community of experts and fellow learners. Our goal is to provide accessible and reliable math support to help you overcome your obstacles and achieve your academic goals.
7.1. Why Choose WHAT.EDU.VN?
- Free Access: Our platform is completely free to use, with no hidden fees or subscriptions.
- Expert Answers: Our community includes experienced mathematicians, teachers, and advanced students who are passionate about helping others.
- Fast Responses: We strive to provide quick and accurate answers to your questions, so you can get the help you need when you need it.
- Community Support: Connect with other learners, share your knowledge, and collaborate on solving challenging math problems.
- Any Question Welcome: No question is too simple or too complex. We’re here to help you with any math problem you encounter.
7.2. How to Get Free Math Help
- Visit WHAT.EDU.VN
- Create a free account or log in if you’re already a member.
- Post your math question in the appropriate category.
- Provide as much detail as possible about the problem, including any relevant background information or attempts you’ve made to solve it.
- Wait for our community of experts to provide answers and guidance.
8. FAQs: Hardest Math Problems
| Question | Answer |
|---|---|
| What makes a math problem “hard”? | Difficulty is subjective, influenced by abstract concepts, multiple steps, unfamiliarity, convoluted wording, and extensive variables. |
| What are some famous unsolved math problems? | The Riemann Hypothesis, Goldbach’s Conjecture, the Twin Prime Conjecture, and the Collatz Conjecture are renowned for their complexity and enduring mystery. |
| What strategies help solve difficult math problems? | Understand fundamentals, break down problems, use diagrams, work backward, identify patterns, use examples, and persist without giving up. |
| How does practice improve math skills? | Regular practice enhances familiarity with problem types and techniques, improving the ability to approach new challenges effectively. |
| Where can I get free math help? | WHAT.EDU.VN offers a platform to ask math questions and receive free answers from experts and fellow learners, providing accessible and reliable support. Feel free to visit us at 888 Question City Plaza, Seattle, WA 98101, United States, or contact us via Whatsapp: +1 (206) 555-7890. Our website is WHAT.EDU.VN. |
9. Overcoming Math Challenges: A Path to Success
While the “hardest” math problem may be a moving target, the journey of tackling challenging mathematical concepts is a rewarding one. By understanding the factors that contribute to difficulty, adopting effective problem-solving strategies, and leveraging available resources like what.edu.vn, you can overcome your math challenges and achieve success in your academic pursuits.
Remember, the goal is not just to find the right answer but to develop your critical thinking, problem-solving, and analytical skills, which will serve you well in all aspects of life. So, embrace the challenges, seek help when needed, and never stop