The quotient is the result you get after dividing one number by another, and at WHAT.EDU.VN, we understand that grasping this concept is crucial for mathematical proficiency. This guide breaks down the quotient definition, explores how to find it, and clarifies its relationship with other division terms, ensuring you have a solid understanding of this foundational mathematical concept. Explore our website WHAT.EDU.VN to ask any questions and get free answers relating to maths topics like long division and even more complex mathematical computations.
1. What Is Quotient in Division?
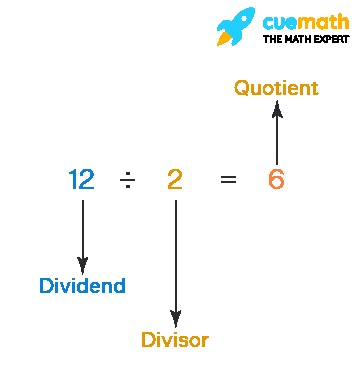
The quotient represents the answer you obtain when you perform division. Division, symbolized by (÷), is a method for distributing items into equal groups. For instance, if you have 15 balls to distribute equally among 3 groups, the division can be written as 15 ÷ 3 = 5. In this case, 5 is the quotient, indicating that each group will contain 5 balls.
2. Quotient Definition
In mathematics, the quotient is defined as the result of dividing a number by a divisor. It indicates how many times the divisor is contained within the dividend. In the division statement, the dividend is the number being divided, the divisor is the number by which you are dividing, and the quotient is the result. The divisor can be larger or smaller than the quotient, but it is consistently smaller than the dividend.
Alt Text: Illustration showing the relationship between dividend, divisor, and quotient in a division problem.
3. How to Find the Quotient
The quotient is determined once the division process is complete. When a divisor divides a dividend, the resulting value is the quotient. Division is a fundamental mathematical operation alongside addition, subtraction, and multiplication. The quotient emerges as the outcome of the division operation. Once a number is divided completely, the quotient is the result. In some instances, division may leave a remainder, yet the quotient remains a distinct part of the answer.
4. Quotient Divisor Dividend
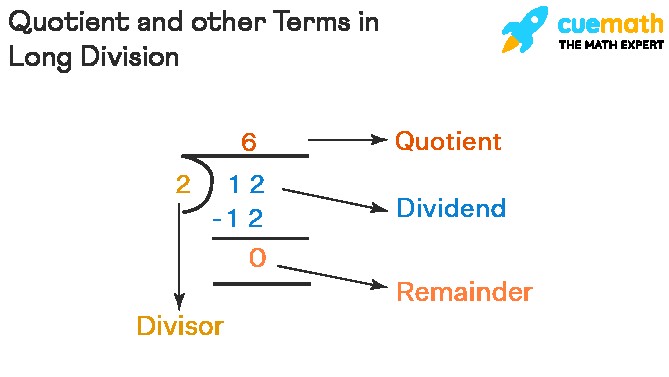
In the process of division, several terms are essential apart from the quotient. Consider a chocolate bar with 12 pieces to understand these terms better. Can this bar be divided equally between two friends? Yes, each friend would receive 6 pieces. In this scenario, no chocolate pieces remain unshared, indicating no remainder. The division statement can be expressed as 12 ÷ 2 = 6. Here’s a breakdown of each term:
| Terms | Descriptions | Values |
|---|---|---|
| Dividend | The total number of pieces to be shared. | 12 |
| Divisor | The number of equal groups to be made. | 2 |
| Quotient | The number of pieces in each group. | 6 |
| Remainder | Any remaining pieces not in a group. | 0 |
This scenario can be mathematically represented as:
Alt Text: Diagram illustrating the roles of the dividend, divisor, quotient, and remainder in a long division problem.
5. Quotient and Remainder
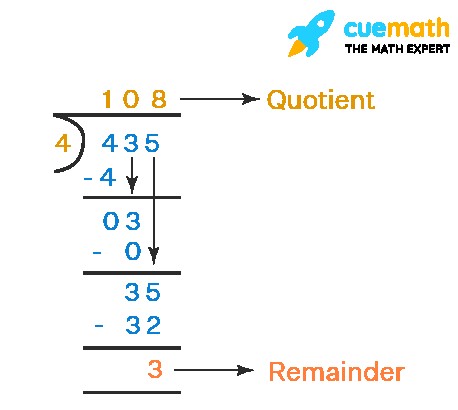
A remainder occurs when a number cannot be divided completely. The quotient is calculated by dividing the dividend by the divisor, using the formula: Quotient = Dividend ÷ Divisor. For example, let’s solve 435 ÷ 4. Here, 435 is the dividend and 4 is the divisor.
The steps below will help you understand how to find both the quotient and the remainder:
- Step 1: Begin with the first digit of the dividend. If it is equal to or larger than the divisor, divide it by the divisor and write the result as part of the quotient. Multiply this number by the divisor and subtract the product from the first digit of the dividend. In this case, 4 ÷ 4 = 1, so 1 is written above the bar. The product of 4 × 1 = 4 is subtracted, resulting in 0. Bring down the next digit, 3, placing it next to 0.
- Step 2: Since 3 is less than 4, it cannot be divided. Write 0 on top and subtract 4 × 0 = 0 from 3, leaving 3. Bring down the next digit, 5, making it 35. As 35 is greater than 4, divide it by 4. Write 8 on top, and then subtract 4 × 8 = 32 from 35, resulting in 3. Since 3 is less than the divisor 4 and no digits are left to bring down, the division is complete with 3 as the remainder and 108 as the quotient.
Alt Text: Step-by-step illustration of long division showing how to determine the quotient and remainder.
Verification of the Division Result
Verify the accuracy of the division using the formula: Dividend = (Divisor × Quotient) + Remainder. This means that if you multiply the divisor by the quotient and add the remainder, the sum should equal the dividend. Reconsidering the previous example, 435 = (4 × 108) + 3 confirms the result.
6. Estimating Quotient
Estimating the quotient involves approximating the quotient by rounding the divisor and dividend to numbers that are easier to compute. To divide 64 ÷ 22 using estimation:
- Step 1: Round the dividend 64 and the divisor 22 to the nearest tens.
- Step 2: 64 rounds down to 60 because the digit in the ones place is less than 5. Similarly, 22 rounds down to 20.
- Step 3: Divide the rounded numbers: 60 ÷ 20 = 3. Therefore, the estimated quotient is 3.
Another estimation method involves eliminating the least number of zeros from both the estimated divisor and dividend. For example, 60 ÷ 20 simplifies to 6 ÷ 2, still resulting in an estimated quotient of 3.
Example: Estimate the quotient of 825 divided by 24.
Solution: To estimate 825 ÷ 24:
- Step 1: Round 825 to the nearest hundred (800) and 24 to the nearest ten (20).
- Step 2: Divide the rounded numbers: 800 ÷ 20 = 40. The estimated quotient is 40.
7. Examples on Quotient
-
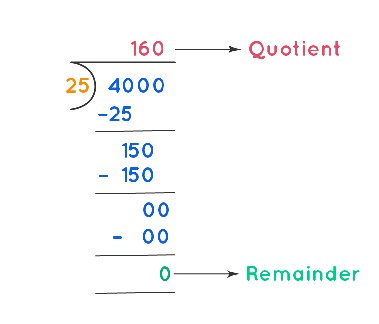
Example 1: $4000 is distributed among 25 workers at a construction site. Calculate the amount each worker receives.
Solution:
Divide the total amount ($4000) by the number of workers (25).
Alt Text: Step-by-step long division showing how to divide $4000 by 25.
The quotient is 160. Each worker receives $160.-
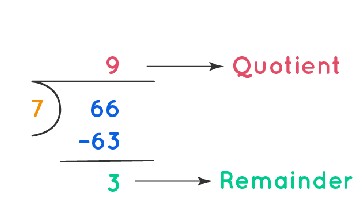
Example 2: Divide 66 ÷ 7 and find the quotient and remainder.
Solution:
Use long division:
Alt Text: Illustration of the long division process for dividing 66 by 7.
The quotient is 9 and the remainder is 3.-
Example 3: State true or false
a.) Quotient is the final answer that we get when we divide a number.
b.) When we divide a number and if it does not get divided completely, we are left with a remainder.
Solution:
a.) True
b.) True
8. Practice Questions on Quotient
Solve the following practice questions to improve your understanding of the quotient.
- Calculate the quotient of 150 divided by 6.
- Determine the quotient and remainder when 235 is divided by 8.
9. FAQs on Quotient
9.1. What is Quotient in Math?
In math, the quotient is the result you get after dividing one number (the dividend) by another (the divisor). For example, in 63 ÷ 9 = 7, the quotient is 7. The quotient can be larger or smaller than the divisor but is always smaller than the dividend.
9.2. How to Find the Quotient in Division?
To find the quotient in division, divide the dividend by the divisor. The formula is: Dividend ÷ Divisor = Quotient. For example, in 12 ÷ 4 = 3, 12 is the dividend, 4 is the divisor, and 3 is the quotient.
9.3. Is Quotient Always a Whole Number?
No, the quotient is not always a whole number. It can be either a whole number or a decimal. In perfect divisions like 16 ÷ 2 = 8, the quotient is a whole number. However, if there is a remainder, such as in 16 ÷ 5 = 3.2, the quotient is a decimal number.
9.4. What is the Difference Between Quotient and Remainder?
The quotient is the result of division, while the remainder is the amount left over when a number cannot be divided completely. For example, if you divide 7 balls among 2 children, each gets 3 balls, and 1 ball is left. Here, 3 is the quotient, and 1 is the remainder.
9.5. How Can We Verify the Quotient in Division?
You can verify the quotient using the formula: Dividend = (Divisor × Quotient) + Remainder. If the result of this equation matches the dividend, the quotient is correct.
9.6. How to Find the Quotient When the Remainder and Divisor is Given?
Given the remainder, divisor, and dividend, use the formula: Dividend = (Divisor × Quotient) + Remainder. Substitute the known values to solve for the quotient.
9.7. What is the Quotient of 21 Divided by 7?
When 21 is divided by 7, the quotient is 3.
9.8. What is the Difference Between Quotient and Product?
The quotient is the result of division, whereas the product is the result of multiplication. The quotient is typically smaller than the dividend, while the product is larger than the numbers being multiplied.
9.9. How to Estimate the Quotient?
To estimate the quotient, round off the divisor and the dividend to numbers that are easy to compute, then divide. For example, to estimate 84 ÷ 18, round 84 to 80 and 18 to 20, then divide 80 ÷ 20 to get an estimated quotient of 4.
Understanding the quotient is fundamental to mastering division. By exploring its definition, learning how to calculate it, and differentiating it from other division terms, you can enhance your mathematical skills and comprehension.
Do you still have questions about the quotient or any other math concepts? Don’t struggle in silence! Visit WHAT.EDU.VN today. We offer a free question-and-answer platform where you can get personalized help from experts. Simply submit your questions, and our knowledgeable community will provide clear, accurate, and helpful answers. Take advantage of our free consultation services to get the academic support you deserve. Reach out to us at 888 Question City Plaza, Seattle, WA 98101, United States, or contact us via WhatsApp at +1 (206) 555-7890. Visit our website what.edu.vn for more information. Ask your questions today and let us help you succeed!
