What Is The Square Root Of 144? A Comprehensive Guide

Are you looking to understand What Is The Square Root Of 144? It’s a fundamental concept in mathematics, and WHAT.EDU.VN is here to simplify it for you. We’ll explore its meaning, calculation methods, and real-world applications. Let’s dive into the world of square roots and discover the solution together, with explanations that are clear and easy to grasp. With WHAT.EDU.VN, unlock the secrets of perfect squares, radical form, and exponential form.

1. Understanding the Basics: What is the Square Root of 144?

The square root of a number is a value that, when multiplied by itself, equals the original number. In simpler terms, if you have a square, the square root of its area is the length of one of its sides. So, what number, when multiplied by itself, gives you 144?

The square root of 144 is 12. Because 12 x 12 = 144. However, it’s important to remember that (-12) x (-12) also equals 144. Therefore, the square root of 144 is both 12 and -12. This concept is fundamental in various areas of mathematics, including algebra, geometry, and calculus. Understanding square roots is crucial for solving equations, simplifying expressions, and tackling real-world problems involving areas and distances.

2. Why is Finding the Square Root of 144 Important?

Understanding the square root of 144, or any number for that matter, extends beyond just knowing the answer. It builds a foundation for more advanced mathematical concepts. Here’s why it’s important:

Foundation for Algebra: Square roots are frequently used in algebraic equations and expressions. Mastering them helps in simplifying complex problems.
Geometry and Measurement: Calculating areas, lengths, and distances often involves square roots. For example, finding the side length of a square when you know its area.
Real-World Applications: Many real-world scenarios, from construction to finance, require the use of square roots for calculations.
Problem-Solving Skills: Working with square roots enhances your problem-solving abilities and logical thinking.
Understanding Perfect Squares: Recognizing perfect squares and their square roots (like 144) is a valuable shortcut in mathematical calculations.

3. Methods to Calculate the Square Root of 144

There are several methods to find the square root of a number. Here are three common methods explained with a focus on finding the square root of 144:

3.1 Prime Factorization Method

This method involves breaking down the number into its prime factors.

Find the Prime Factors: First, find the prime factors of 144.
- 144 = 2 x 2 x 2 x 2 x 3 x 3
- This can be written as 2⁴ x 3²
Group the Factors in Pairs: Group the prime factors into pairs of identical numbers.
- 144 = (2 x 2) x (2 x 2) x (3 x 3)
- This can be written as 2² x 2² x 3²
Take One Factor from Each Pair: Take one number from each pair and multiply them together.
- √144 = 2 x 2 x 3 = 12
- Therefore, the square root of 144 is 12.

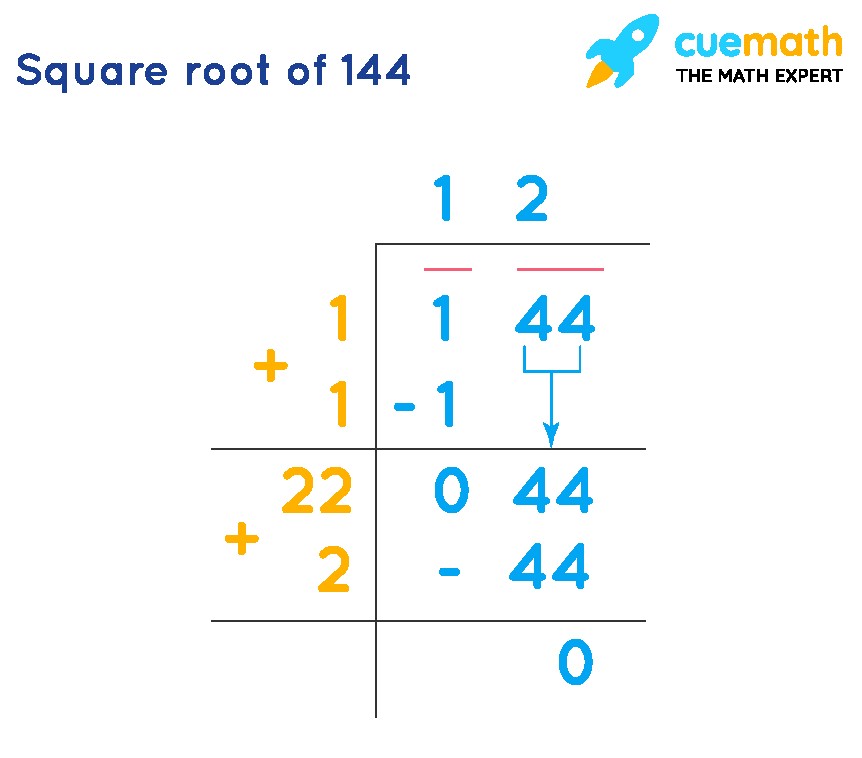
3.2 Long Division Method

This is a more methodical approach, especially useful for larger numbers.

Write the Number: Write 144 and pair the digits from right to left.
- In this case, it’s 1 44 (1 is considered a single entity).
Find the Largest Square: Find the largest number whose square is less than or equal to the leftmost digit or pair (which is 1 in this case).
- 1 x 1 = 1
- Write 1 as the divisor and the quotient.
Subtract and Bring Down: Subtract the product from the leftmost digit and bring down the next pair (44).
- The new dividend is 44.
Double the Quotient: Double the quotient (1) and write it as the new divisor’s ten’s place digit (2_).
Find the Unit Digit: Find a digit to place in the unit’s place of the divisor such that the product of the new divisor and this digit is equal to or less than the new dividend (44).
- In this case, 2 x 2 = 4, so the digit is 2.
- The new divisor is 22.
Multiply and Subtract: Multiply the new divisor (22) by the digit (2) and subtract from the dividend (44).
- 22 x 2 = 44
- 44 – 44 = 0
Result: The quotient (12) is the square root of 144.

Long division method example showing how to calculate the square root of 144

3.3 Repeated Subtraction Method

This method involves repeatedly subtracting consecutive odd numbers from the original number until you reach zero. The number of steps it takes to reach zero is the square root.

Start Subtracting Odd Numbers: Begin subtracting consecutive odd numbers from 144.
- 144 – 1 = 143
- 143 – 3 = 140
- 140 – 5 = 135
- Continue this pattern.
Count the Steps: Keep track of how many times you subtract.
- 135 – 7 = 128
- 128 – 9 = 119
- 119 – 11 = 108
- 108 – 13 = 95
- 95 – 15 = 80
- 80 – 17 = 63
- 63 – 19 = 44
- 44 – 21 = 23
- 23 – 23 = 0
Determine the Square Root: The number of steps taken to reach zero is the square root.
- In this case, it took 12 steps.
- Therefore, the square root of 144 is 12.

4. Square Root of 144: Rational or Irrational?

Understanding whether the square root of a number is rational or irrational is crucial in mathematics. A rational number can be expressed as a fraction p/q, where p and q are integers and q is not zero. An irrational number cannot be expressed in this form.

Since the square root of 144 is 12 (or -12), which can be written as 12/1 (or -12/1), it is a rational number. Rational numbers include all integers, fractions, and terminating or repeating decimals. Irrational numbers, on the other hand, are non-terminating and non-repeating decimals, such as √2 or π.

5. Practical Applications of the Square Root of 144

The concept of the square root of 144 isn’t just theoretical; it has several practical applications in everyday life. Here are a few examples:

Construction and Design: Architects and engineers use square roots to calculate dimensions of square or rectangular structures. For instance, if you’re designing a square room with an area of 144 square feet, you need to know that each side should be 12 feet long.
Gardening and Landscaping: If you’re planning a square garden, knowing the square root of the desired area helps you determine the length of the sides. A 144 square foot garden would have sides of 12 feet each.
Home Improvement: When tiling a square area, such as a bathroom floor, understanding square roots helps you calculate how many tiles you need. If the area is 144 square feet and each tile is 1 square foot, you’ll need 144 tiles, arranged in a 12×12 grid.
Photography and Image Editing: In digital imaging, square roots are used in resizing and scaling images while maintaining proportions.
Navigation and Mapping: Calculating distances and areas on maps often involves the use of square roots.
Manufacturing: In manufacturing processes, square roots are used to determine the dimensions of square or cubic products.

6. Common Mistakes to Avoid When Calculating Square Roots

When working with square roots, it’s easy to make mistakes if you’re not careful. Here are some common errors to avoid:

Forgetting the Negative Root: Always remember that every positive number has two square roots: a positive root and a negative root. For example, both 12 and -12 are square roots of 144.
Confusing Square Root with Division: The square root is not the same as dividing a number by 2. The square root is a value that, when multiplied by itself, equals the original number.
Incorrect Prime Factorization: Ensure you correctly identify the prime factors when using the prime factorization method.
Misapplying the Long Division Method: Follow each step of the long division method carefully to avoid errors in calculation.
Assuming All Square Roots are Rational: Not all square roots are rational. For example, the square root of 2 is an irrational number.
Calculator Dependency: While calculators are useful, relying on them entirely without understanding the underlying concepts can lead to mistakes.
Ignoring Units: When dealing with real-world problems, remember to include the appropriate units in your answer (e.g., feet, meters, inches).
Rounding Errors: Be cautious when rounding off square roots, especially in intermediate steps, as it can affect the final result.

7. Examples of Square Root of 144 in Action

Let’s look at some real-world examples that demonstrate how the square root of 144 is used:

7.1 Building a Patio

Imagine you’re building a square patio in your backyard. You want the patio to have an area of 144 square feet. To determine how long each side of the patio should be, you need to find the square root of 144.

Area of patio = 144 square feet
Side length = √144 = 12 feet
Therefore, each side of the patio should be 12 feet long.

7.2 Creating a Quilt

Suppose you’re making a square quilt, and you want the finished quilt to have an area of 144 square inches. To figure out how big each side of the quilt should be, you need to calculate the square root of 144.

Area of quilt = 144 square inches
Side length = √144 = 12 inches
Each side of the quilt should be 12 inches long.

7.3 Designing a Garden Bed

You’re designing a square garden bed, and you want it to cover 144 square meters. To determine the length of each side, you need to find the square root of the area.

Area of garden bed = 144 square meters
Side length = √144 = 12 meters
Each side of the garden bed should be 12 meters long.

8. Advanced Concepts Related to Square Roots

While understanding the basics of square roots is essential, delving into more advanced concepts can further enhance your mathematical knowledge. Here are a few related topics:

Cube Roots: Similar to square roots, cube roots involve finding a number that, when multiplied by itself three times, equals the original number.
Higher Order Roots: This includes fourth roots, fifth roots, and so on. The nth root of a number is a value that, when raised to the nth power, equals the original number.
Complex Numbers: The square roots of negative numbers are complex numbers. For example, the square root of -1 is denoted as “i”.
Radical Expressions: These are expressions that contain square roots or other radicals. Simplifying radical expressions involves removing perfect square factors from the radicand (the number under the radical sign).
Rationalizing the Denominator: This technique involves eliminating radicals from the denominator of a fraction.
Square Root Functions: These are functions that involve square roots, such as f(x) = √x. Understanding these functions is crucial in calculus and advanced algebra.
Approximating Square Roots: When dealing with non-perfect squares, it’s important to know how to approximate their square roots using methods like the Babylonian method or numerical techniques.

9. The Square Root of 144 in Different Number Systems

The concept of square roots is consistent across different number systems. Here’s how the square root of 144 is represented in some common number systems:

Decimal (Base 10): In our everyday number system, the square root of 144 is 12.
Binary (Base 2): In binary, 144 is represented as 10010000. The square root, 12, is represented as 1100.
Hexadecimal (Base 16): In hexadecimal, 144 is represented as 90. The square root, 12, is represented as C.
Roman Numerals: In Roman numerals, 144 is represented as CXLIV. The square root, 12, is represented as XII.

Understanding how numbers and their square roots are represented in different number systems is crucial in computer science and other fields that deal with data representation.

10. Tips and Tricks for Mastering Square Roots

Mastering square roots can be easier with the right strategies and practice. Here are some tips and tricks to help you improve your skills:

Memorize Perfect Squares: Knowing the perfect squares (1, 4, 9, 16, 25, 36, 49, 64, 81, 100, 121, 144, etc.) and their square roots can save you time and effort.
Practice Regularly: The more you practice, the more comfortable you’ll become with square roots.
Use Flashcards: Create flashcards with perfect squares on one side and their square roots on the other.
Break Down Complex Problems: When faced with a complex problem involving square roots, break it down into smaller, more manageable steps.
Check Your Answers: Always double-check your answers to avoid careless errors.
Understand the Concepts: Don’t just memorize formulas; make sure you understand the underlying concepts.
Apply Real-World Examples: Relate square roots to real-world situations to make them more meaningful and easier to remember.
Use Online Resources: Take advantage of online resources like tutorials, videos, and practice quizzes.
Seek Help When Needed: Don’t hesitate to ask for help from teachers, tutors, or classmates if you’re struggling with square roots.

11. The History of Square Roots

The concept of square roots dates back to ancient civilizations. The Babylonians, for example, had methods for approximating square roots as early as 1800 BC. They used algorithms similar to the modern-day Babylonian method for approximating square roots.

The ancient Greeks also made significant contributions to the understanding of square roots. Pythagoras and his followers explored the relationship between square roots and geometry, particularly in the context of right triangles.

The concept of square roots was further developed in India and the Islamic world. Indian mathematicians like Aryabhata and Brahmagupta made advancements in calculating square roots and using them in astronomical calculations. Islamic scholars translated and preserved many Greek and Indian mathematical texts, contributing to the continued study of square roots.

In Europe, the study of square roots was revived during the Renaissance. Mathematicians like Leonardo Fibonacci helped to popularize the Hindu-Arabic numeral system and the use of square roots in algebra and geometry.

12. Fun Facts About Square Roots

Here are some interesting and fun facts about square roots:

The symbol for square root, “√”, is called a radical symbol. It originated from the letter “r,” which stands for “radix” (the root of a number).
The square root of a prime number is always an irrational number.
The square root of a negative number is an imaginary number.
The square root of 0 is 0.
The square root of 1 is 1.
The Babylonian method for approximating square roots is an iterative algorithm that converges quickly to the correct answer.
Square roots are used in computer graphics to calculate distances and create realistic 3D models.
The concept of square roots is used in cryptography to encrypt and decrypt secret messages.

13. FAQ: Square Root of 144

13.1 What is the square root of 144?

The square root of 144 is 12, because 12 multiplied by itself (12 x 12) equals 144. Additionally, -12 multiplied by itself (-12 x -12) also equals 144, so -12 is also a square root of 144.

13.2 Is the square root of 144 a rational or irrational number?

The square root of 144 is a rational number because 12 can be expressed as a fraction (12/1).

13.3 How do you find the square root of 144 using prime factorization?

Find the prime factors of 144: 2 x 2 x 2 x 2 x 3 x 3
Group the factors in pairs: (2 x 2) x (2 x 2) x (3 x 3)
Take one factor from each pair: 2 x 2 x 3 = 12

13.4 Can the square root of 144 be negative?

Yes, the square root of 144 can be negative. Both 12 and -12 are square roots of 144 because 12 x 12 = 144 and -12 x -12 = 144.

13.5 What are some real-world applications of the square root of 144?

The square root of 144 is used in construction, gardening, home improvement, photography, and mapping to calculate dimensions, areas, and distances.

13.6 What is the exponential form of the square root of 144?

The exponential form of the square root of 144 is 144^1/2.

13.7 What is the radical form of the square root of 144?

The radical form of the square root of 144 is √144.

13.8 How can I approximate the square root of a number that is not a perfect square?

You can approximate the square root of a non-perfect square using methods like the Babylonian method or numerical techniques.

13.9 What is the difference between a square and a square root?

Squaring a number means multiplying it by itself (e.g., 12² = 144). Finding the square root of a number means finding a value that, when multiplied by itself, equals the original number (e.g., √144 = 12).

13.10 Is the square root of -144 a real number?

No, the square root of -144 is not a real number. It is an imaginary number, represented as 12i.

14. Conclusion: Mastering the Square Root of 144

Understanding what is the square root of 144 and its applications is a foundational element in mathematics. From its calculation methods to its real-world uses, the concept of square roots is essential for problem-solving and logical thinking.

If you have more questions or need further assistance with any mathematical concepts, don’t hesitate to reach out to us at WHAT.EDU.VN. We offer free consultations and answers to all your questions. Contact us at 888 Question City Plaza, Seattle, WA 98101, United States, or via WhatsApp at +1 (206) 555-7890. You can also visit our website at WHAT.EDU.VN for more information. Let what.edu.vn be your go-to resource for all your educational needs!

A student learning and researching with a laptop