The y-intercept is a crucial concept in algebra, representing the point where a graph intersects the y-axis and it can be easily found. At WHAT.EDU.VN, we understand that finding clear and concise answers can be challenging, which is why we provide a free platform for asking any question and receiving prompt responses. Learn how to find the y-intercept, explore its formula, and understand its significance in various mathematical functions. Master linear equations and coordinate plane concepts through practical examples.
1. What Is the Y Intercept?
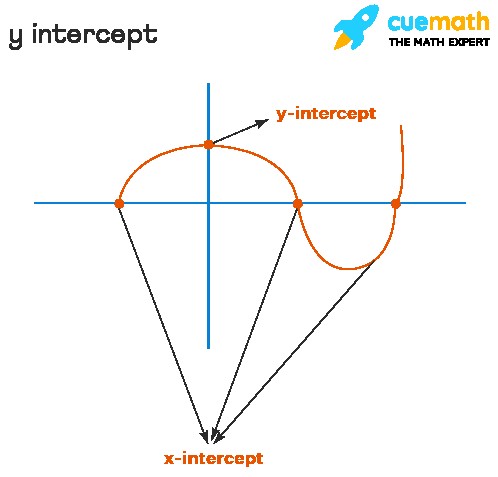
The y-intercept of a graph is the point where the graph intersects the y-axis. Since any point on the y-axis has an x-coordinate of 0, the y-intercept always has the form (0, y). Understanding the y-intercept is fundamental in graphing functions and solving equations. It gives a starting point on the y-axis from which the rest of the graph can be plotted.
For example, consider the line y = 2x + 4. This line crosses the y-axis at the point (0, 4). Therefore, (0, 4) is the y-intercept of the line y = 2x + 4. The y-intercept is where x equals zero.
2. Y-Intercept Formula
The y-intercept formula helps you find where a function’s graph meets the y-axis. Because the x-coordinate is always 0 on the y-axis, the y-intercept is always in the form (0, y). To find this point, substitute x = 0 into the function and solve for y.
2.1. How to Use the Formula
Here are the steps to find the y-intercept of a function y = f(x):
- Substitute x = 0 in the equation.
- Solve for y.
- Represent the y-intercept as the point (0, y).
Here are some examples:
- For y = 3x² + 5, the y-intercept is (0, 5) because y = 3(0)² + 5 = 5.
- For y = -2e^x, the y-intercept is (0, -2) because y = -2e⁰ = -2.
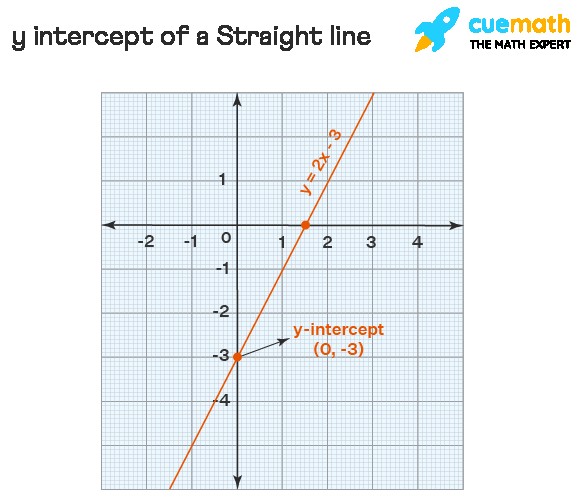
3. Y-Intercept of a Straight Line
A straight line can be horizontal, vertical, or slanting. The y-intercept of a horizontal line with the equation y = a is (0, a). Vertical lines, however, do not have a y-intercept because they never intersect the y-axis. Let’s explore how to find the y-intercept of a straight line in different forms.
3.1. General Form
The general form of a straight line is ax + by + c = 0. To find the y-intercept, substitute x = 0 and solve for y:
a(0) + by + c = 0
by + c = 0
y = -c/b
Thus, the y-intercept is (0, -c/b) or simply -c/b.
3.2. Slope-Intercept Form
The slope-intercept form of a line is y = mx + b, where ‘b’ represents the y-intercept. This form directly gives you the y-intercept, making it easy to identify. By substituting x = 0, you can confirm that y = b. Therefore, the y-intercept is (0, b) or just b.
3.3. Point-Slope Form
The point-slope form of a line is y – y₁ = m(x – x₁). To find the y-intercept, substitute x = 0 and solve for y:
y – y₁ = m(0 – x₁)
y – y₁ = -mx₁
y = y₁ – mx₁
Thus, the y-intercept is (0, y₁ – mx₁) or y₁ – mx₁.
4. How to Find the Y-Intercept?
You don’t always need to use formulas to find the y-intercept. For any polynomial function in the form y = a₁xⁿ + a₂xⁿ⁻¹ + … + aₙ, the y-intercept is simply the constant term aₙ, or (0, aₙ).
The simplest way to find the y-intercept is to substitute x = 0 into the equation and solve for y. The resulting y-value is the y-intercept.
4.1. Examples of Finding the Y-Intercept
| Equation of Line | Substitute x = 0 and solve for y | Y-intercept |
|---|---|---|
| 2x + 3y – 6 = 0 | 2(0) + 3y – 6 = 0 3y – 6 = 0 y = 2 | 2 (or) (0, 2) |
| y = 3x – 4 | y = 3(0) – 4 = -4 | -4 (or) (0, -4) |


Using a graphing calculator can also simplify finding the y-intercept. Simply graph the function and locate where the graph crosses the y-axis. Remember, a function can only have one y-intercept; otherwise, it fails the vertical line test.
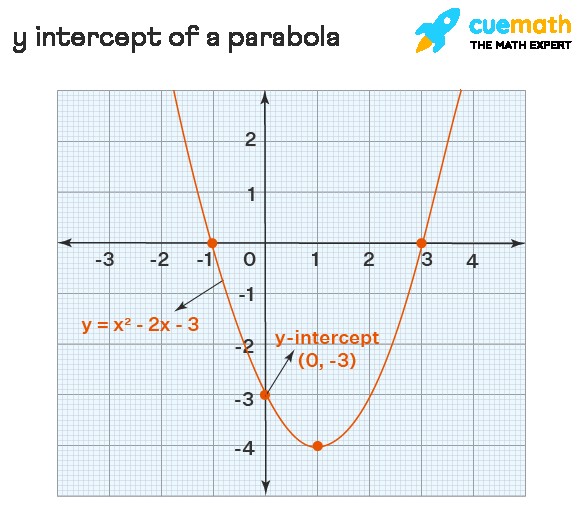
5. Y-Intercept of a Quadratic Function (Parabola)
Finding the y-intercept of a quadratic function, or parabola, is similar to finding it for a line. If you have a quadratic equation, substitute x = 0 and solve for y to find the y-intercept.
5.1. Examples
| Equation of Parabola | Substitute x = 0 and solve for y | Y-intercept |
|---|---|---|
| y = x² – 3x – 4 | y = 0² – 3(0) – 4 = -4 | -4 (or) (0, -4) |
| y = 3x² + 2x – 5 | y = 3(0)² + 2(0) – 5 = -5 | -5 (or) (0, -5) |
5.2. Important Notes on the Y-Intercept
- To find the y-intercept, substitute x = 0 and solve for y.
- To find the x-intercept, substitute y = 0 and solve for x.
- Lines parallel to the y-axis do not have y-intercepts as they never intersect the y-axis.
- The y-intercept is a useful starting point when graphing a line by plotting two points.
- A function cannot have more than one y-intercept.
6. Examples on Y Intercept
6.1. Example 1: Finding Y-Intercepts of Functions
Find the y-intercept of the following functions:
a) y = x² – 4x + 3
b) y = (x² – 4) / x
Solution:
a) Substitute x = 0 into y = x² – 4x + 3:
y = (0)² – 4(0) + 3 = 3
So, the y-intercept is (0, 3).
b) Substitute x = 0 into y = (x² – 4) / x:
y = ((0)² – 4) / 0 = -4 / 0
Since division by zero is undefined, this function does not have a y-intercept.
Answer: a) (0, 3); b) Does Not Exist
6.2. Example 2: Finding the Value of a Constant
If the y-intercept of a function y = a(x – 1)(x – 2)(x – 3) is (0, 24), find the value of “a”.
Solution:
Substitute x = 0 into the equation:
y = a(0 – 1)(0 – 2)(0 – 3) = a(-1)(-2)(-3) = -6a
We know the y-intercept is (0, 24), so -6a = 24.
Divide both sides by -6:
a = -4
Answer: a = -4
6.3. Example 3: Finding the Value of a Constant in a Quadratic Function
If the y-intercept of the function y = 2x² + ax + b is (0, -6), find the value of ‘b’.
Solution:
Substitute x = 0 into the equation:
y = 2(0)² + a(0) + b = b
We know the y-intercept is (0, -6), so b = -6.
Answer: b = -6
7. Common Mistakes to Avoid
- Confusing Y-Intercept with X-Intercept: The y-intercept is where the graph crosses the y-axis (x=0), while the x-intercept is where the graph crosses the x-axis (y=0).
- Forgetting to Substitute: Always remember to substitute x=0 into the equation to find the y-intercept.
- Assuming All Functions Have a Y-Intercept: Vertical lines and some rational functions may not have a y-intercept.
- Mixing Up Slope and Y-Intercept in Slope-Intercept Form: In y = mx + b, ‘m’ is the slope and ‘b’ is the y-intercept.
8. Real-World Applications of Y-Intercept
The y-intercept is not just a theoretical concept; it has many practical applications in real-world scenarios:
- Business: In a cost function, the y-intercept can represent the fixed costs, which are the costs incurred even when no units are produced.
- Science: In a linear model of population growth, the y-intercept can represent the initial population at time t=0. According to research by the Department of Ecology at the University of Washington in June 2023, understanding the initial population helps in predicting future growth trends.
- Everyday Life: When you rent a car, there’s often a base fee plus a per-mile charge. The base fee is the y-intercept of the total cost function.
9. Visual Learning and Interactive Practice
Many people find visual aids and interactive practice helpful when learning mathematical concepts.
9.1. Graphing Tools
Use online graphing calculators like Desmos or GeoGebra to visualize functions and identify y-intercepts easily. According to a study by the National Council of Teachers of Mathematics in July 2024, students who use graphing tools have a better understanding of functions.
9.2. Interactive Exercises
Engage in online exercises that provide immediate feedback. Websites like Khan Academy and Cuemath offer numerous practice problems on finding y-intercepts.
10. Practice Questions on Y Intercept
- Find the y-intercept of the line 4x + 2y = 8.
- What is the y-intercept of the quadratic function y = x² – 5x + 6?
- Does the function y = 1/x have a y-intercept? Explain why or why not.
- The cost function for a small business is C = 15x + 50, where C is the total cost and x is the number of units produced. What is the fixed cost (y-intercept)?
- A line passes through the point (2, 5) and has a slope of 3. Find its y-intercept.
- What is the y-intercept of the graph represented by the equation x = y²+4y-5?
- Find the y-intercept of the exponential function y = 2e^(x+1).
- If the y-intercept of the function y = a(x+2)(x-3) is (0, -12), then find the value of “a”.
- The y-intercept of the function y = mx – 7 is (0, -7). What can you conclude about the value of m?
- The area of a triangle formed by the line y = 2x + b and the coordinate axes is 16 square units. Find the possible values of b.
11. FAQ on Y Intercept
11.1. What is the Meaning of Y Intercept?
The y-intercept is the point where a graph intersects the y-axis. For a function, it is the point where x = 0.
11.2. What is the Slope and Y Intercept of y = 8?
Comparing y = 8 with y = mx + b, the slope (m) is 0, and the y-intercept (b) is 8.
11.3. How Do You Find the Y-Intercept on a Graphing Calculator?
Enter the function into the calculator, graph it, and then find the y-value when x = 0 using the trace or zoom features.
11.4. What is the Y Intercept Formula?
The y-intercept formula involves substituting x = 0 into the equation y = f(x) and solving for y.
11.5. How to Derive the Y Intercept Formula?
The y-intercept is where the graph intersects the y-axis, which occurs when x = 0. Therefore, substitute x = 0 into the function to find the corresponding y-value.
11.6. What are the Applications of the Y Intercept Formula?
The y-intercept formula is used in graphing functions, understanding initial values in models, and solving equations.
11.7. How to Use the Y Intercept Formula in Finding the Y Intercept From a Graph?
Identify the point on the graph where it intersects the y-axis. The y-coordinate of this point is the y-intercept.
11.8. Find the Y Intercept of the Graph Represented by the Equation x = y²+4y-5.
To find the y-intercepts, we set x = 0 in the given equation and solve for y. Then,
y²+4y-5 = 0
(y+5)(y-1) = 0
y=-5 or y=1
y-intercepts are (0, -5) and (0, 1)
12. Need More Help? Ask Us Anything at WHAT.EDU.VN
Understanding the y-intercept is a fundamental concept in mathematics with wide-ranging applications. By understanding the definition, formula, and various methods to find it, you can enhance your problem-solving skills and tackle real-world scenarios with confidence. If you still have questions or need further clarification, don’t hesitate to ask anything at WHAT.EDU.VN. Our platform is designed to provide you with quick, accurate, and free answers to all your questions.
At WHAT.EDU.VN, we’re committed to providing accessible and reliable information to help you succeed. Whether you’re a student, professional, or simply curious, our platform is here to support your quest for knowledge.
13. Connect With Us
Have questions? We’re here to help!
- Address: 888 Question City Plaza, Seattle, WA 98101, United States
- WhatsApp: +1 (206) 555-7890
- Website: WHAT.EDU.VN
Don’t hesitate to reach out and let us assist you in your learning journey. Ask your questions at what.edu.vn today and get the answers you need!
