Prime numbers are fundamental in mathematics, acting as the basic building blocks for all other whole numbers. Understanding what prime numbers are is crucial not just for math students, but for anyone curious about the nature of numbers themselves. In simple terms, a prime number is a whole number greater than 1 that has only two divisors: 1 and itself.
Let’s break this down. Consider the number 7. You can only divide 7 evenly by 1 and 7. There are no other whole numbers that divide into 7 without leaving a remainder. This makes 7 a prime number. Now, think about the number 8. You can divide 8 by 1, 2, 4, and 8. Because 8 has more than two divisors, it is not a prime number. Instead, it’s known as a composite number. The number 1 itself is special; it only has one divisor (which is 1), so by definition, it is not a prime number either. It’s in a category of its own.
Defining Prime Numbers {#defining-prime-numbers}
To formally define a prime number, we can say: A prime number is a natural number greater than 1 that has exactly two positive divisors: 1 and itself.
This definition is critical. Let’s unpack it further:
- Natural Number: Prime numbers are within the set of natural numbers, which are the positive whole numbers (1, 2, 3, …).
- Greater than 1: The number 1 is excluded from being a prime number because it only has one divisor.
- Exactly Two Divisors: This is the defining feature. If a number has more or less than two divisors, it’s not prime.
For example, consider 11. Its only divisors are 1 and 11. Therefore, 11 fits the definition of a prime number. On the other hand, consider 12. Its divisors are 1, 2, 3, 4, 6, and 12. Since 12 has more than two divisors, it is not a prime number; it’s a composite number.
Characteristics of Prime Numbers {#characteristics-of-prime-numbers}
Prime numbers have several interesting properties that set them apart:
- Fundamental Theorem of Arithmetic: Every integer greater than 1 can be uniquely expressed as a product of prime numbers, or is itself a prime number. This is a cornerstone of number theory, highlighting the foundational role of primes. For example, 12 can be broken down into 2 × 2 × 3 (2² × 3), and these are all prime factors.
- Infinitude of Primes: There is no largest prime number. Euclid proved this over 2000 years ago, demonstrating that prime numbers go on forever. This concept is fundamental to understanding the vastness of numbers.
- Distribution of Primes: While prime numbers are infinite, their distribution becomes less frequent as numbers get larger. The Prime Number Theorem describes this distribution, stating that the probability of a random number near n being prime is approximately 1/ln(n), where ln(n) is the natural logarithm of n.
- Unique Even Prime: The number 2 is the only even prime number. All other even numbers are divisible by 2 and therefore have more than two divisors (1, 2, and themselves at least).
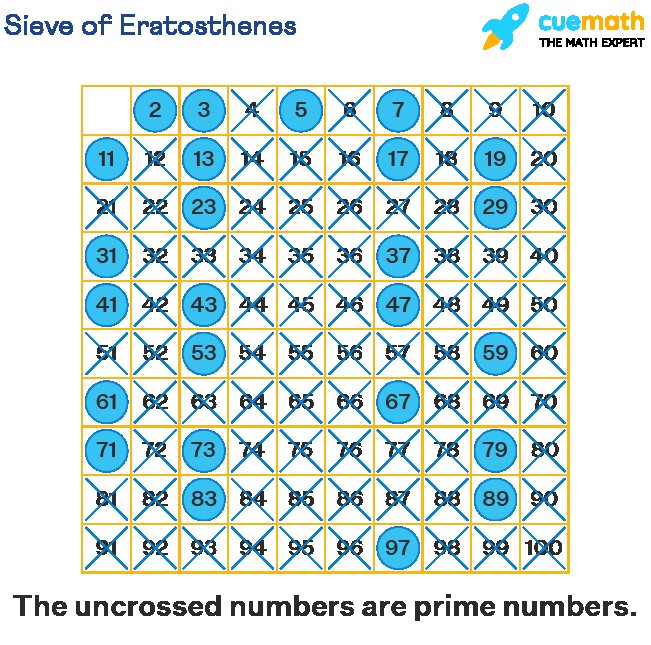Sieve of Eratosthenes for finding prime numbers up to 100
Prime Numbers vs. Composite Numbers {#prime-numbers-vs-composite-numbers}
The number system can be broadly categorized into prime numbers, composite numbers, and the unique number 1. We’ve already defined prime numbers. Let’s clarify composite numbers:
- Composite Numbers: A composite number is a natural number greater than 1 that has more than two positive divisors. In essence, they are numbers that can be formed by multiplying two smaller natural numbers.
Here’s a table summarizing the key differences:
| Feature | Prime Numbers | Composite Numbers |
|---|---|---|
| Definition | Exactly two divisors (1 and itself) | More than two divisors |
| Factors | Limited to 1 and the number itself | At least three factors |
| Number 1 | Not prime | Not composite |
| Smallest | 2 | 4 |
| Even Numbers | Only 2 is prime | All other even numbers are composite |
| Examples | 2, 3, 5, 7, 11, 13, 17, 19, 23, 29, 31, etc. | 4, 6, 8, 9, 10, 12, 14, 15, 16, 18, 20, etc. |
Prime Numbers and Co-prime Numbers {#prime-numbers-and-co-prime-numbers}
It’s easy to confuse prime numbers with co-prime numbers, but they are distinct concepts.
- Co-prime Numbers (Relatively Prime): Two numbers are said to be co-prime or relatively prime if their greatest common divisor (GCD) is 1. This means they share no common positive factors other than 1.
Key differences:
- Prime Number: Refers to a single number with specific divisor properties.
- Co-prime Numbers: Describes a relationship between two or more numbers.
- Condition for Co-prime: Co-prime numbers only require that their GCD is 1. They do not both need to be prime numbers themselves.
Examples to illustrate:
- 5 and 9 are co-prime: The factors of 5 are 1, 5. The factors of 9 are 1, 3, 9. Their only common factor is 1. Note that 5 is prime, but 9 is composite.
- 8 and 15 are co-prime: Factors of 8 are 1, 2, 4, 8. Factors of 15 are 1, 3, 5, 15. Again, only common factor is 1. Both 8 and 15 are composite.
- 7 and 11 are co-prime: Factors of 7 are 1, 7. Factors of 11 are 1, 11. Both are prime, and they are also co-prime.
Essentially, any two different prime numbers will always be co-prime. However, co-prime numbers do not have to be prime themselves.
Finding Prime Numbers: Methods {#finding-prime-numbers-methods}
Identifying whether a number is prime, especially for larger numbers, can be challenging. Here are a few methods:
-
Trial Division: This is the most straightforward method for smaller numbers. To check if a number n is prime, divide it by all prime numbers less than or equal to the square root of n. If none of these primes divide n evenly, then n is prime.
- Example: Is 37 prime? √37 is approximately 6. Prime numbers less than 6 are 2, 3, 5. 37 is not divisible by 2, 3, or 5. Therefore, 37 is prime.
-
Sieve of Eratosthenes: An ancient algorithm for finding all prime numbers up to a specified integer. We’ll detail this method in a later section.
-
Fermat’s Little Theorem (Probabilistic Test): This theorem provides a probabilistic primality test. If p is a prime number, then for any integer a, the number ap – a is an integer multiple of p. While helpful, it’s not foolproof as some composite numbers (Carmichael numbers) can also satisfy this condition.
-
More Advanced Primality Tests: For very large numbers, more sophisticated tests like the Miller-Rabin primality test or the AKS primality test are used. These are essential in cryptography and computer science.
For everyday purposes and understanding, trial division and the Sieve of Eratosthenes are typically sufficient.
Odd Prime Numbers: An Overview {#odd-prime-numbers-an-overview}
With the exception of the number 2, all prime numbers are odd. This is because any even number greater than 2 is, by definition, divisible by 2, and therefore has more than two factors (1, 2, and itself at least), making it composite.
The sequence of odd prime numbers starts as: 3, 5, 7, 11, 13, 17, 19, 23, 29, 31, and continues infinitely.
It’s important to remember that while all prime numbers except 2 are odd, not all odd numbers are prime. For example, 9, 15, 21, 25, 27 are odd numbers but are composite.
The History and Mystery of Prime Numbers {#the-history-and-mystery-of-prime-numbers}
Prime numbers have fascinated mathematicians for millennia. Their seemingly random distribution among integers, coupled with their fundamental role in number theory, has made them a subject of intense study and intrigue.
- Ancient Greeks: The study of prime numbers dates back to ancient Greece. Euclid, around 300 BC, proved the infinitude of primes. Eratosthenes developed the Sieve of Eratosthenes, a method still used today to find prime numbers.
- Goldbach’s Conjecture: One of the oldest and most famous unsolved problems in number theory, proposed in 1742, states that every even integer greater than 2 can be expressed as the sum of two primes. Despite extensive research, a definitive proof remains elusive.
- Riemann Hypothesis: Another major unsolved problem concerning the distribution of prime numbers is linked to the Riemann zeta function. Its solution carries a million-dollar prize and would have profound implications for our understanding of prime distribution.
- Modern Applications: Prime numbers are not just theoretical curiosities. They are crucial to modern cryptography. Algorithms like RSA (Rivest-Shamir-Adleman) encryption rely heavily on the properties of large prime numbers to secure online communication and transactions. The difficulty of factoring large numbers into their prime factors is what makes these encryption methods secure.
Sieve of Eratosthenes: A Prime Number Tool {#sieve-of-eratosthenes-a-prime-number-tool}
The Sieve of Eratosthenes is a simple, ancient algorithm for finding all prime numbers up to any given limit. Here’s how it works:
- Create a list: Write down all integers from 2 to your chosen limit.
- Start with the first prime: The first number in the list, 2, is prime.
- Mark multiples: Cross out all multiples of 2 in the list (4, 6, 8, etc.).
- Move to the next unmarked number: The next number that is not crossed out is the next prime number (which is 3).
- Repeat: Cross out all multiples of this new prime number (6, 9, 12, etc.).
- Continue: Repeat steps 4 and 5, moving to the next unmarked number each time, until you have processed all numbers up to the square root of your limit.
- The primes remain: All numbers remaining in the list that are not crossed out are prime numbers.
This method effectively ‘sieves out’ the composite numbers, leaving only the primes.
go to slidego to slidego to slide
Key Facts About Prime Numbers {#key-facts-about-prime-numbers}
To summarize, here are some important facts about prime numbers:
- Smallest Prime: The smallest prime number is 2.
- Even Prime: 2 is the only even prime number.
- First Few Primes: The first five prime numbers are 2, 3, 5, 7, and 11.
- Number 1: 1 is neither prime nor composite.
- Infinitude: There are infinitely many prime numbers.
- Odd Primes: All prime numbers except 2 are odd.
- Building Blocks: Prime numbers are the building blocks of all other whole numbers (Fundamental Theorem of Arithmetic).
☛ Related Topics:
| Is 1 a Prime Number? | Is 2 a Prime Number? |
|---|---|
| Is 5 a Prime Number? | Is 7 a Prime Number? |
| Is 9 a Prime Number? | Is 11 a Prime Number? |
| Is 13 a Prime Number? | Is 17 a Prime Number? |
| Is 19 a Prime Number? | Is 23 a Prime Number? |
| Is 29 a Prime Number? | Is 31 a Prime Number? |
| Is 37 a Prime Number? | Is 41 a Prime Number? |
| Is 43 a Prime Number? | Is 47 a Prime Number? |
| Is 49 a Prime Number? | Is 51 a Prime Number? |
| Is 57 a Prime Number? | Is 59 a Prime Number? |
| Is 61 a Prime Number? | Is 63 a Prime Number? |
| Is 67 a Prime Number? | Is 71 a Prime Number? |
| Is 79 a Prime Number? | Is 83 a Prime Number? |
| Is 89 a Prime Number? | Is 91 a Prime Number? |
| Is 97 a Prime Number? | Is 101 a Prime Number? |
Frequently Asked Questions About Prime Numbers {#frequently-asked-questions-about-prime-numbers}
Q1: What are prime numbers in math?
A: In mathematics, prime numbers are natural numbers greater than 1 that are only divisible by 1 and themselves. They are the fundamental building blocks of all other integers. Examples include 2, 3, 5, 7, 11, and so on.
Q2: Can you give some examples of prime numbers?
A: Sure, here are a few examples of prime numbers: 2, 3, 5, 7, 11, 13, 17, 19, 23, 29, 31, 37, 41, 43, 47, 53, 59, 61, 67, 71, 73, 79, 83, 89, 97, 101, 103, 107, 109, 113, and the list goes on infinitely.
Q3: How can I determine if a number is prime?
A: For smaller numbers, trial division is effective. Divide the number by prime numbers less than or equal to its square root. If none divide evenly, it’s prime. For larger numbers, more advanced primality tests are needed.
Q4: Why is 2 considered a prime number?
A: The number 2 is prime because it fits the definition: it is greater than 1 and has exactly two positive divisors, which are 1 and 2 itself. It’s also unique as the only even prime number.
Q5: What is the list of all prime numbers from 1 to 100?
A: The prime numbers between 1 and 100 are: 2, 3, 5, 7, 11, 13, 17, 19, 23, 29, 31, 37, 41, 43, 47, 53, 59, 61, 67, 71, 73, 79, 83, 89, and 97.
Q6: What’s the smallest prime number?
A: The smallest prime number is 2.
Q7: What differentiates a prime and a co-prime number?
A: A prime number is a single number with only two divisors. Co-prime numbers are a pair of numbers that have no common factors other than 1. Prime numbers are about individual divisibility, co-prime numbers are about the relationship between two numbers.
Q8: Can prime numbers be negative?
A: By definition, prime numbers are natural numbers, which are positive whole numbers greater than 1. Therefore, prime numbers cannot be negative.
Q9: What are twin prime numbers?
A: Twin prime numbers are pairs of prime numbers that differ by 2, such as (3, 5), (5, 7), (11, 13), and so on.
Q10: Are prime numbers always odd?
A: No, prime numbers are not always odd. The number 2 is a prime number and it is even. In fact, 2 is the only even prime number. All other prime numbers are odd.
Q11: What are numbers that are not prime called?
A: Numbers that are not prime (and are greater than 1) are called composite numbers. These numbers have more than two factors.
Q12: Is there a largest prime number?
A: No, there is no largest prime number. Prime numbers are infinite, as proven by Euclid.
Q13: Which is the first prime number?
A: The first prime number is 2.
Q14: Are there any even prime numbers between 1 and 100?
A: Yes, there is one even prime number between 1 and 100, and that is 2. It is the only even prime number in the entire set of prime numbers.
Q15: What is the largest prime number between 1 and 10?
A: The largest prime number between 1 and 10 is 7.
Quick Quiz:
Q1: Choose the prime number from these options: 4, 7, 9, 15.
Q2: How many factors does a prime number have?
Q3: Which number is the only even prime number?
Q4: A prime number is divisible only by _____ and itself.
Q5: The greatest common factor (GCF) of any two different prime numbers is always _____.
