In mathematics, understanding different types of numbers is fundamental. Among these, rational numbers play a crucial role. You encounter them every day, often without even realizing it! But what’s a rational number exactly?
Simply put, a rational number is any number that can be expressed as a fraction or a ratio of two integers. This fraction takes the form p/q, where ‘p’ and ‘q’ are integers, and importantly, ‘q’ (the denominator) is not equal to zero.
Think of it like slicing a pizza. If you cut a pizza into ‘q’ equal slices and take ‘p’ of those slices, the portion you have can be represented by the rational number p/q.
Common examples of rational numbers include:
- Fractions: ½, ¾, -2/5, 10/3. Any fraction you can think of with a non-zero denominator is a rational number.
- Integers: …-3, -2, -1, 0, 1, 2, 3… Wait, integers? Yes! Any integer can be written as a fraction with a denominator of 1. For example, 5 can be written as 5/1, and -7 can be written as -7/1. Even zero (0) is a rational number because it can be expressed as 0/1, 0/2, 0/3, and so on.
- Terminating Decimals: 0.5, 0.75, 1.25, -0.3. These decimals end after a finite number of digits. Terminating decimals can always be converted into fractions (e.g., 0.5 = 1/2, 0.75 = 3/4).
- Repeating Decimals: 0.333…, 1.666…, 2.142857142857… These decimals have a pattern of digits that repeats infinitely. Repeating decimals can also be expressed as fractions (e.g., 0.333… = 1/3, 0.142857… = 1/7).
However, it’s equally important to understand what is not a rational number. Numbers like 1/0, 5/0, or any number divided by zero are not rational numbers. Division by zero is undefined in mathematics, leading to an infinite result, which does not fit the definition of a rational number.
To further explore numbers that are not rational, you might want to learn about irrational numbers. Understanding irrational numbers helps to fully grasp the scope of rational numbers by highlighting their differences.
Let’s delve deeper into the characteristics and properties of rational numbers.
Identifying Rational Numbers: Key Conditions
How can you definitively identify if a number is rational? Here are the key conditions to check:
- Can it be written in the form p/q? This is the fundamental test. If you can express the number as a fraction where both ‘p’ and ‘q’ are integers and ‘q’ is not zero, then it’s rational.
- Does its decimal representation terminate or repeat? If you convert a rational number into a decimal, it will either terminate (end) or repeat a sequence of digits infinitely. Conversely, if a decimal representation neither terminates nor repeats, it is not a rational number (it’s irrational).
Key takeaways for identifying rational numbers:
- Rational numbers encompass positive numbers, negative numbers, and zero.
- They can always be represented as a fraction.
- Their decimal form is either terminating or repeating.
Consider these examples:
| p | q | p/q | Rational? | Decimal Form | Decimal Type |
|---|---|---|---|---|---|
| 10 | 2 | 10/2 = 5 | Yes | 5.0 | Terminating |
| 1 | 1000 | 1/1000 = 0.001 | Yes | 0.001 | Terminating |
| 50 | 10 | 50/10 = 5 | Yes | 5.0 | Terminating |
| 1 | 3 | 1/3 | Yes | 0.333… | Repeating |
| -7 | 2 | -7/2 | Yes | -3.5 | Terminating |

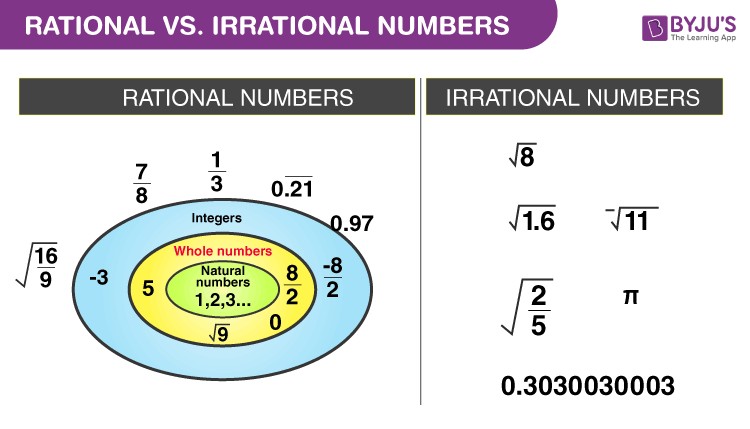

Types of Rational Numbers: Exploring the Subsets
Rational numbers are part of a larger family of numbers, and they themselves contain smaller, important sets. Understanding these relationships helps to clarify the position of rational numbers within the number system.
The diagram below illustrates the hierarchy of number sets:
- Real Numbers (R): This is the broadest category, including all rational numbers and irrational numbers.
- Rational Numbers (Q): As we’ve defined, numbers expressible as p/q.
- Integers (Z): Whole numbers and their negatives (…-2, -1, 0, 1, 2…). All integers are rational.
- Whole Numbers (W): Non-negative integers (0, 1, 2, 3…). All whole numbers are rational.
- Natural Numbers (N): Positive integers (1, 2, 3…). All natural numbers are rational.
Key Relationships:
- Every natural number is a whole number, an integer, and a rational number.
- Every whole number is an integer and a rational number.
- Every integer is a rational number.
- Not every rational number is an integer (e.g., 1/2 is rational but not an integer).
- Not every real number is a rational number (irrational numbers exist).
Standard Form of Rational Numbers: Simplification
A rational number is in its standard form (or simplest form) when two conditions are met:
- The numerator and denominator have no common factors other than 1. This means the fraction has been simplified as much as possible.
- The denominator is positive.
For example, consider the rational number 12/36. It’s rational, but it’s not in standard form because 12 and 36 share common factors (like 2, 3, 4, 6, and 12). To convert it to standard form, we simplify it by dividing both numerator and denominator by their greatest common divisor, which is 12.
12 ÷ 12 = 1
36 ÷ 12 = 3
So, the standard form of 12/36 is 1/3. Here, 1 and 3 have no common factors other than 1, and the denominator (3) is positive.
Positive and Negative Rational Numbers: Sign Matters
Rational numbers can be positive or negative, just like integers and real numbers.
- Positive Rational Numbers: A rational number p/q is positive if both the numerator (p) and the denominator (q) have the same sign (both positive or both negative). For example, 3/5 and -2/-7 are positive rational numbers. All positive rational numbers are greater than 0.
- Negative Rational Numbers: A rational number p/q is negative if the numerator (p) and the denominator (q) have opposite signs (one positive and one negative). For example, -2/5 and 3/-7 are negative rational numbers. All negative rational numbers are less than 0.
It’s important to note that:
-(p/q) = (-p)/q = p/(-q)
This means the negative sign can be placed in front of the fraction, with the numerator, or with the denominator, and the value remains the same.
| Positive Rational Numbers | Negative Rational Numbers |
|---|---|
| Numerator and denominator have the same sign. | Numerator and denominator have opposite signs. |
| All are greater than 0. | All are less than 0. |
| Examples: 12/17, 9/11, 3/5, -4/-6 | Examples: -2/17, 9/-11, -1/5, -6/7 |
Arithmetic Operations on Rational Numbers: Working with Fractions
Just like with integers, we can perform basic arithmetic operations (addition, subtraction, multiplication, and division) on rational numbers. Let’s explore how these operations work for two rational numbers, p/q and s/t.
Addition: To add two rational numbers, p/q and s/t, we need to find a common denominator. The easiest common denominator is the product of the denominators (q*t).
p/q + s/t = (p*t + q*s) / (q*t)
Example: 1/2 + 3/4 = (1*4 + 2*3) / (2*4) = (4 + 6) / 8 = 10/8 = 5/4 (simplified)
Subtraction: Subtraction is similar to addition; we also need a common denominator.
p/q – s/t = (p*t – q*s) / (q*t)
Example: 1/2 – 3/4 = (1*4 – 2*3) / (2*4) = (4 – 6) / 8 = -2/8 = -1/4 (simplified)
Multiplication: Multiplying rational numbers is straightforward. We multiply the numerators together and the denominators together.
(p/q) * (s/t) = (p*s) / (q*t)
Example: 1/2 * 3/4 = (1*3) / (2*4) = 3/8
Division: Dividing by a rational number is the same as multiplying by its reciprocal (multiplicative inverse). To divide p/q by s/t, we flip the second fraction (s/t) to become (t/s) and then multiply.
(p/q) ÷ (s/t) = (p/q) * (t/s) = (p*t) / (q*s)
Example: 1/2 ÷ 3/4 = (1/2) * (4/3) = (1*4) / (2*3) = 4/6 = 2/3 (simplified)
Multiplicative Inverse (Reciprocal) of Rational Numbers
The multiplicative inverse or reciprocal of a rational number p/q is simply q/p (where p is not zero). When you multiply a rational number by its multiplicative inverse, the result is always 1.
(p/q) * (q/p) = 1
Example: The multiplicative inverse of 4/7 is 7/4. And indeed, (4/7) * (7/4) = 28/28 = 1.
Properties of Rational Numbers: How They Behave
Rational numbers, as a subset of real numbers, follow many of the same fundamental properties. These properties are important for understanding how rational numbers behave under different operations.
- Closure Property: Rational numbers are closed under addition, subtraction, and multiplication. This means that if you add, subtract, or multiply any two rational numbers, the result will always be another rational number.
- Commutative Property: Addition and multiplication of rational numbers are commutative. This means the order doesn’t matter:
- p/q + s/t = s/t + p/q
- (p/q) * (s/t) = (s/t) * (p/q)
- Associative Property: Addition and multiplication of rational numbers are associative. This means grouping doesn’t matter:
- (p/q + s/t) + u/v = p/q + (s/t + u/v)
- ((p/q) * (s/t)) * (u/v) = (p/q) * ((s/t) * (u/v))
- Identity Property:
- Additive Identity: 0 is the additive identity for rational numbers. Adding 0 to any rational number doesn’t change its value: p/q + 0 = p/q.
- Multiplicative Identity: 1 is the multiplicative identity for rational numbers. Multiplying any rational number by 1 doesn’t change its value: (p/q) * 1 = p/q.
- Distributive Property: Multiplication distributes over addition for rational numbers:
- (p/q) * (s/t + u/v) = (p/q) * (s/t) + (p/q) * (u/v)
- Density Property: Between any two distinct rational numbers, there are infinitely many other rational numbers. This is a unique property of rational numbers (and real numbers).
You can explore these properties of rational numbers in more detail to deepen your understanding.
Rational Numbers and Irrational Numbers: A Clear Distinction
Rational numbers are contrasted with irrational numbers. The key difference is that irrational numbers cannot be expressed in the form of a simple fraction p/q, where p and q are integers and q is not zero.
Key Differences:
| Feature | Rational Numbers | Irrational Numbers |
|---|---|---|
| Fraction Form (p/q) | Yes, can be expressed as p/q | No, cannot be expressed as p/q |
| Decimal Representation | Terminating or Repeating | Non-terminating and Non-repeating |
| Examples | ½, -3/4, 0.5, 0.333…, 7 | π (pi), √2, √3, e (Euler’s number), 0.1010010001… |
Irrational numbers, when written as decimals, go on forever without repeating any pattern. Famous examples of irrational numbers include:
- Pi (π): Approximately 3.141592653589… This is the ratio of a circle’s circumference to its diameter.
- Square root of 2 (√2): Approximately 1.41421356… This is the length of the diagonal of a square with side length 1.
- Euler’s Number (e): Approximately 2.718281828459… This number is important in calculus and other areas of mathematics.
Finding Rational Numbers Between Two Rational Numbers: Infinite Possibilities
A consequence of the density property is that there are infinitely many rational numbers between any two given rational numbers. Here are two common methods to find rational numbers between two given rational numbers.
Method 1: Using Equivalent Fractions
- Find a common denominator: Convert the two given rational numbers to equivalent fractions with a common denominator.
- Increase the denominator (if needed): If the numerators are consecutive integers or too close, increase the denominator by multiplying both the numerator and denominator of each fraction by the same integer (e.g., 2, 3, 10, etc.). This creates more “space” between the fractions.
- Identify intermediate rational numbers: Once you have fractions with a larger common denominator and sufficient space between numerators, you can easily identify rational numbers with the same denominator whose numerators fall between the numerators of your two fractions.
Method 2: The Mean (Average) Method
- Find the mean: Calculate the average of the two given rational numbers by adding them together and dividing by 2. This mean value will always be a rational number that lies between the two original numbers.
- Repeat (for more numbers): To find more rational numbers, you can repeat the process. Take the mean of one of the original numbers and the newly found mean. You can continue this process to find as many rational numbers as you need.
Example: Find a rational number between 1/4 and 1/2.
Method 1 (Equivalent Fractions):
- Common denominator: 1/4 and 2/4 (1/2 = 2/4)
- Increase denominator (multiply by 2): 2/8 and 4/8
- Intermediate rational number: 3/8 (which is between 2/8 and 4/8)
Method 2 (Mean Method):
- Mean: (1/4 + 1/2) / 2 = (1/4 + 2/4) / 2 = (3/4) / 2 = 3/8
Both methods show that 3/8 is a rational number between 1/4 and 1/2. You can find many more by repeating these methods.
Solved Examples: Putting Knowledge into Practice
Let’s work through some examples to solidify your understanding of rational numbers.
Example 1: Identify as Rational or Irrational
Classify each of the following numbers as rational or irrational: ¾, 90/12007, 12, and √5.
Solution:
- ¾: Rational. It is already expressed as a fraction p/q. Decimal form is 0.75 (terminating).
- 90/12007: Rational. It is expressed as a fraction p/q.
- 12: Rational. It can be written as 12/1 (fraction form). Decimal form is 12.0 (terminating).
- √5: Irrational. The square root of 5 is a non-terminating, non-repeating decimal (approximately 2.236…). It cannot be expressed as a simple fraction.
Example 2: Mixed Fraction – Is it Rational?
Is the mixed fraction 1 ½ a rational number?
Solution:
First, convert the mixed fraction to an improper fraction: 1 ½ = (1*2 + 1) / 2 = 3/2.
3/2 is in the form p/q, where p=3 and q=2 are integers and q≠0. Therefore, 1 ½ is a rational number.
Example 3: Decimal to Rational Conversion
Determine whether the given decimal numbers are rational or irrational: (a) 1.75 (b) 0.01 (c) 0.5 (d) 0.09 (e) √3
Solution:
Convert each decimal to fraction form if possible:
| Decimal Number | Fraction Form | Rational? |
|---|---|---|
| 1.75 | 175/100 = 7/4 | Yes |
| 0.01 | 1/100 | Yes |
| 0.5 | 5/10 = 1/2 | Yes |
| 0.09 | 9/100 | Yes |
| √3 | Cannot be expressed as a simple fraction | No (Irrational) |
Frequently Asked Questions About Rational Numbers
Q1: What are rational numbers? Give examples.
A: A rational number is a number that can be expressed in the form of p/q, where p and q are integers, and q is not equal to 0. Examples include: 1/3, 2/4, 1/5, 9/3, -5/2, 0, 7.
Q2: What is the difference between rational and irrational numbers?
A: Rational numbers can be expressed as a ratio of two integers (fractions), and their decimal representations either terminate or repeat. Irrational numbers cannot be expressed as simple fractions, and their decimal representations are non-terminating and non-repeating. Examples: Rational (10/2), Irrational (π).
Q3: Is 0 a rational number?
A: Yes, 0 is a rational number. It can be written as 0/1, 0/2, etc., satisfying the p/q form where q is non-zero.
Q4: Is 7 a rational number?
A: Yes, 7 is a rational number. It can be written as 7/1, fitting the definition of a rational number.
Q5: Is 3.14 a rational number? What about π?
A: 3.14 is a rational number because it’s a terminating decimal (314/100). However, π (pi) is an irrational number. While 3.14 is a common approximation for π, the actual value of π is a non-terminating, non-repeating decimal (approximately 3.141592653589793238…).
Q6: Find a rational number between 3 and 4.
A: One rational number between 3 and 4 is their mean: (3+4)/2 = 7/2 or 3.5.
Q7: What is the denominator of a rational number?
A: The denominator of a rational number (q in p/q) can be any integer except 0.
Q8: Is Pi (π) a rational number?
A: No, Pi (π) is not a rational number. It is a famous irrational number with a non-terminating, non-repeating decimal representation.
Understanding rational numbers is a foundational step in mathematics. They are essential for everyday calculations, further mathematical studies, and various applications in science and engineering. By grasping their definition, properties, and operations, you build a strong base for more advanced mathematical concepts.

